The Pyramids of Meroe, 1821
Even now much attention continues to be afforded to the pyramids of Egypt, particularly those of Giza, but seemingly much less is given to the Nubian pyramids, in spite of their appearance in prominent works like Mark Lehner’s The Complete Pyramids.
Primarily five sites are under discussion as being the location of groups of these diminutive, steep sided pyramids – El Kurra, Nuri, Jebel Barkal, Napata, and especially Meroe.
The Pyramids of Meroe from Mark Lehner, “The Complete Pyramids“
For me, one of the great questions is whether the mathematics we seem to find at Giza can be expected to be intrinsic to these pyramids as well. Obviously, the Nubian pyramids reflect considerable Egyptian influence on Nubian architecture, but did Egypt also have mathematical and metrological influence on Nubian pyramids, and if what the Egyptian were doing with pyramidal architecture was a tradition, did that tradition continue as late as the Nubian Pyramids?
The Nubian pyramids are also intriguing because of the attached temples, which often also feature pylons resembling the pylons seen in Egyptian architecture. I have a certain curiosity about the mathematical and geometric nature of these pylons that thus far remains unfulfilled curiosity because of a general lack of data about them. Unfortunately, I’m not certain if I’ve acquired any data sets that would give a lower / upper width or thickness ratio for one of these taped pylon structures, but their appearance in Nubian architecture theoretically gives us more chances that we might obtain a study of them.
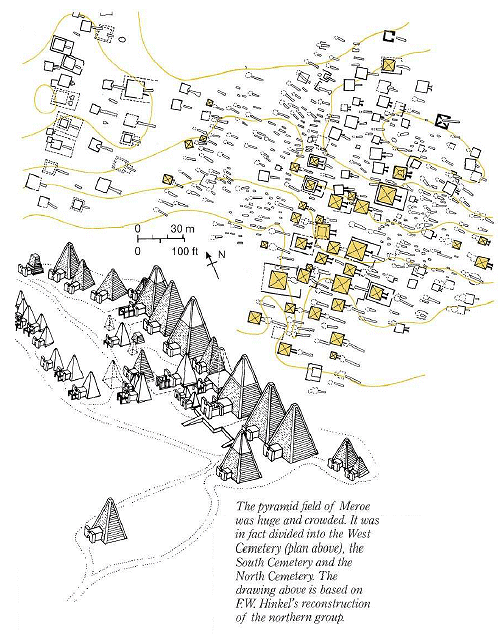
Pyramid temples at Meroe fronted by Pylons, several of which have been reconstructed by FW Hinkel.
At present the data sets I have for Nubian pyramids are, sadly, incomplete as those for Egyptian pyramids often are, but even then there are some interesting glimmers, and given the attention paid to the Nubian pyramids by archaeologists with a special focus on them, there may well be more data out there somewhere.
A diagram of one of Meroe’s pyramids by FW Hinkel is available on-line in a publication by the Sudan Archaeological Research Association.
Cover feature on Nubian pyramids: Hinkel, F. W. 2000. ‘The Royal Pyramids of Meroe. Architecture, Construction and Reconstruction of a Sacred Landscape’, Sudan & Nubia 4, 11-26.
I’ve made several attempts to work with Hinkel’s data in hopes of a more complete model, but my confidence level in parts of the model is relatively concerning the parts of it which are left to mathematical projection or archaeological reconstruction partly because of destruction that a number of the Nubian pyramids have suffered , both of which feel somewhat uncomfortably speculative. On the other hand, projective geometry has worked well to date with Egyptian pyramids, and the parts of Hinkel’s model that are less speculative are fascinating of themselves.
Reduced version of Hinkel’s diagram of one of the pyramids of Meroe, the pyramid attributed to Taktidamani
Hinkel gives the total with of the platform as 7.40 m, and the width of the entrance as 1.52 m. There is 15 cm noted on either side of the pyramid as the distance from the top of the platform to the pyramid base, giving then the pyramid base as 7.40 m – (.15 x 2 m) = 7.10 m.
7.40 m = 24.2781522 ft; 1.52 m = 4.986876640 ft; .15 m = .4922125984 ft; 7.10 m = 23.299396325.
24.2781522 / 20 = 1.213907610, giving a suggestion that either a very advanced astronomical value might have been in use, or perhaps more simply and more plausibly, the Egyptian Remen of normally 1.216733603 ft. 1.216733603 x 20 = 24.33467206 ft, a difference of .05652 ft or about 2/3 of one inch overall.
The ratio between platform and pyramid widths from the data is 7.40 / 7.10 = 1.042253521. While this could mean one of a number of calendrical constants, it’s also suggestive of 1/3 of Pi, often a very powerful data retrieval tool as is evidenced at many ancient sites.
24.33467206 / (Pi / 3) = 23.23790008. This is the square root of 540, an important and powerful mathematical constant, and a simple fraction or multiple of more constants whose utility and importance is often even more dramatic. That’s important to keep in mind because the figure might easily be mistaken for 13 1/2 Royal Cubits (13.5 x 1.72 = 23.22), but the role of the Remen here and the value of the platform / pyramid ratio may offer guidance and reassurance here concerning other viable possibilities.
23.23790008 is 1/2 of 46.47580016 (sqrt 2160), which I have long proposed to be the intended length of the burial chamber inside the pyramid of Chephren (Khafre) at Giza. We can expect to see figures like these associated with pyramids and related architecture often enough, although metrologically they may remain somewhat of a mystery.
Just as we can tell that the ancient Egyptians were extremely fond of 1.067438159 as both a mathematical constant and metrological unit (in “modern” feet), yet the name that the ancient Egyptians called this remains elusive although it is an apparent subdivision of the Egyptian Royal Foot (the nomenclature thus defaults to “Hashimi Cubit” since it is older than the “Pied du Roi”), the only thing currently in my metrological lexicon to relate 46.47580016 and 23.23790008 to is Prof. Thom’s Mid-Clythe Quantum, which I take to be sqrt 60 feet.
sqrt 60 x 3 = 23.23790008 ft; sqrt 60 x 6 = 46.47580016 ft
Since the metrology may thus remain somewhat problematic, we can instead focus on the mathematical values.
Something that I find rather intriguing is that the slope angle of this pyramid is that from Hinkel’s diagram it measures almost exactly, and presumably is, 60 degrees. As previously mentioned, I am indebted to Bogna Krys for putting the concept before me of expressing angle values in radians. I’m surprised that I did not think of it without further prompting since some of Prof. Thom’s work on Megalithic Ring types also expresses angle values in radians. What is very encouraging about the concept is that is able to turn what seem like rather plain pyramid angle values into something powerful and exciting.
The radian value is 360* / (2 Pi) = 57.29577951 – again, the Great Pyramid seems to be most of all literally a massive advertisement for this with the Royal Cubit (.03 Radians feet = .03 x 57.29577951 = 1.718873385) corroborating this proposition.
In Radians, 60 degrees = 60* / 57.29577951 = 1.047197551, 1/3 of Pi, putting the amazing data retrieval tool and data series facilitator (Pi / 3) within ready reach of a number of Egyptian pyramids thought to have such angles.
Thus, what these suggestions amount to is that a possible platform / pyramid base ratio of Pi / 3 may be corroborated by the value of the accompanying slope angle value in Radians. This may also be an emphatic that tells us that (Pi / 3) may be SO important here that they want to make doubly sure that its presence isn’t overlooked. (In such cases, we may have also been intended to examine the square root of the slope angle – that too is very important, because sqrt 60 is currently the most powerful data storage and retrieval tool known).
I’d almost prefer to keep the discussion focused on geometry and metrology since ancient geodesy no doubt remains a very controversial subject some, but to be forthright, it was during earlier work with Hinkel’s plan for this pyramid that some absolutely stunning geodetic facts about the square root of 60 first came to light, after being “right under our noses” for a very long time. That was all that had to happen was to simply ask if these Nubian pyramids might exhibit the same geodetic tendencies that Egypt’s pyramids seem to exhibit, and a series of revelations began.
Another potentially controversial aspect of the same pyramid is that ratio between platform width and entrance according to data is 7.40 / 1.52 = 4.86842153, which is surprisingly close to the value of 4 Remens in feet. This seems to be a very common feature of ancient Egyptian architecture, to find values of metrological units in feet written as ratios between parts as if they are built-in instructions concerning ancient unit values, in values in “modern” feet, another apparently rather ancient metrological unit that we seem to be hard pressed to find historical names for.
1.216733603 x 4 = 4.86694411 (and yes, this is 1/10 of the inner radius of the Stonehenge sarcen circle). 1.52 m = 4.986876640 ft. We might subject this to further scrutiny, but to accept the parameters attempted thus far, if 7.40 m = 24.2781522 ft means 1.216733603 x 20 = 24.33467206,
24.33467206 / 4.86694411 = 5.000000000
If the series of assumptions that lead to this are correct, the width of the entrance of pyramid BEG W 18 may be 5 “Imperial” feet, although such blatant use of the foot in ancient times may be extremely rare. The “Modern” foot is much more valuable as a reference unit that gives extraordinary values to to other units. It may mean that there is a number or series of numbers formed from 5 and either (Pi / 3) or sqrt 60 that the designers wished to incorporate or wanted any would-be interpreters to find.
While I’m uncomfortable projecting data much further from pixel measurements, if the base and slope angle have been correctly identified (George Reisner reported at least 4 more Nubian pyramids at Nuri with slope angles measured at 60*), we might at least try projecting the slope to the height of an apex point (even if such a thing was never actually an original feature of the pyramid given the curious style of the capstones associated with them).
The projected slope (the hypotenuse of the triangle) is equal to twice the base of the triangle, which is 1/2 of the length of one side of the base of the pyramid. The projected height appears to be in “Palestinian Cubits”, i.e., 10 Palestinian Cubits of 2.107038476 ft each, accuracy .999807376, above the “Giza Standard” minimum of accuracy for approximations forced by the effects of geometry and algebra or addition and subtraction on metrological unit values).
I frequently put “Palestinian Cubit” in quotation marks as I do with other expressions when I wish to question the validity of such labels. Technically, the “Palestian Cubit” is the diagonal to a rectangle with short sides of 1 Remen and long sides of 1 Royal Cubit, the two primary ancient Egyptian units of measure.
The perimeter / height ratio that would result from this would be 4.619692775, which may be less than ideal (hence the style of capstones which would actually give the pyramid a different height in “real life”?), but this figure does have meaning = for example, 2 / 4.619692775 = 4329.2922222 / 10^n, which appears to be a particularly useful approximation of Jupiter’s Orbital Period of 4332.59 days. (The Orbital Period of Saturn is even easier to find here since Thom’s “Mid Clythe Quantum” is ideally suited to its expression).
Since that is about all the further I would like to go for now with data projections based on Hinkel’s plan, I will draw things to a close for this part. The other thing I could do is lay out elaborate displays of the constants that can be formed from even the few values given here, but just how impressive some of the resulting series can be is something the reader can easily find out for themselves with your average pocket calculator.
I would like to suggest, however, that if we have a “mandate” (or at least a “license”) to apply 2 Pi to all pyramids because 2 Pi is the perimeter / height ratio of their “Mothership”, the Great Pyramid, it may certainly be in evidence here for the wealth of data it may be able to extract from the resident pyramid architecture.
–Luke Piwalker