Many references have been made to possible values for an ancient meter. An ancient Meter very much like the modern meter is an idea that seems to occur to numerous researchers into ancient mathematics and metrology, myself included. I’ve been experimenting with the idea for more years than I’d like to admit, but it still isn’t clear to me what would be the primary intended value for an ancient Meter the way it is with other units.
1.216733603 and 1.718873385 are very obviously the primary values for the Egyptian Remen and Egyptian Royal Cubit respectively, 1.177245771 and 1.067438159 are very obviously the primary values for the Megalithic Foot and Hashimi Cubit respectively, and so on – but what the primary value for an ancient Meter would be seems to remain mysterious.
A number of candidates for an ancient form of the (1 / .0348 = 3.280839895) ft Meter have been known for a long time, including the “Radian Squared Meter” (Radian 57.29577951)^2 / 1000 = 3.282806350 ft, and the “Shaved Meter” 3.282806350 / 1.000723277 = 3.280433687 ft.
The “Radian Squared Meter” differs from the contemporary Meter value by 3.282806350 – 3.280839895 = 0.001966454645 ft or 0.001966454645 x 12 = 0.023597455 inches, about 2/10ths of 1/10th of an inch, and the “Shaved Meter” of course differs from the modern Meter by even less.
A possible formula has been noted that may link some ancient Meters to the Egyptian Remen, which is 4 / Remen = ~1 Meter.
4 / 1.216733603 = 3.287490368
4 / 1.215854204 = 3.289868134
4 / 1.218469679 = 3.282806351
4 / 1.219350970 = 3.280433687
It seems uncertain whether 1.219350970 was recognized as a form of the Remen or whether this would be “mixing metaphors” mathematically. Likewise, 3.287490368 hasn’t seemed to attract all that much support as an ancient Meter and may simply be another expression of standard Remens of 1.216733603 ft.
1.218469679 is the so-called “Thoth Remen”, so-called because Our Founder Carl Munck made a big deal out of the number 9 and its reciprocal (along with the number 240 and its square root) being symbols of “Thoth, Father of Number”, and demonstrated that if we square the reciprocal of 9, it produces all the numbers (except 8) in the correct order
1 / 9 = .1111111111; .1111111111^2 = 1.234567901 / 100, making “Thoth” the “Father of Numbers” literally.
Michael Morton and I also discovered that if we multiply this by the number missing from the sequence, 8, we get all the numbers in descending order
1.234567901 x 8 = 9.876543210
This wonderful phenomenon doesn’t seem to see all that much usage, largely because 2 / 1.234567901 = 162/100, which is far too easily overshadowed by more powerful and more useful numbers like 2 / 1.622311470 = 1.232808888 or 2 / 1.618829140 = 1.235460834, and yet it is part of our vocabulary.
Finally, 1.234567901 x (Pi^2) = 12.18469679, or 10 “Thoth Remens”, and that is why the name was used.
We see in the list one of 1.218469679’s claims to legitimacy, which is
4 / 1.218469679 = 3.282806351, which is equivalent to 4 / (360 / (1.718873385^2)). Because basic circular geometry, involving the 360* degree circle, 2 Pi, and 360 / (2 Pi) = Radian 57.29577951, it’s a fairly strong vote of confidence for the legitimacy of 1.218469679 as an actual Egyptian Remen Value, no matter how little use it may see for being greatly overshadowed by the two most important forms of the Remen, 1.216733603 and 1.215854204.
This may bring us to a struggle for “primacy” between 4 / 1.215854204 = 3.289868134 and 4 / 1.218469679 = 3.282806351.
Certainly it’s a huge vote of confidence for the possible legitimacy of 3.289868134 as an ancient Meter value that such a figure is technically the same as the “Short Remen” of 1.215854204 ft, but it’s a difficult battle between the important circular geometry origin of 3.282806351 and the relatedness of 3.289868134 to the “Short Remen” as to whether 3.282806351 or 3.289868134 is the first Meter value we should try when confronted with a possible ancient Meter.
3.289868134 may have something important going for it which may not, which is exponential value.
For example, while 3.282806351 ft is currently thought to be the intended width of the Stonehenge sarsen circle (outer diameter 103.9030303 ft – inner diameter 97.33868822 ft = 2 x 3.282171039 ft, which can represent 3.282806351 but cannot represent 3.289868134, as accurately as we would prefer to require, we nonetheless have only to drop 3.289868134 into this situation to see some of what it’s capable of
2.733689474 x 3.289868134 = 29.58741331 = 4 Squared Munck Meg Yards
29.58741331 x 3.289868134 = 97.33868822 = 80 Remens in ft
97.33868822 x 3.289868134 = 320.2314486 = 300 Hashimi Cubits in ft
320.2314486 x 3.289868134 = 1053.519238 = 500 Palestinian Cubits in ft
1053.519238 x 3.289868134 = 346.5939370 x 10^n, preferred Eclipse Year
So we not only see exponential value in excess of that of most metrological units from 3.289868134 here, but we see that it is directly linking other metrological units to each other, and to the preferred Eclipse Year value, which should put it on at least equal footing with a possible meter of 3.282806351, which should be hard pressed to show such exponential value even for being an exponent of the Radian.
3.289868134 has been considered as a possible meter for long enough that it’s tried to take on several names. It’s been called the “Guachimontones Meters” before because in his paper on one of the Guachmontones circular step pyramids, Dimitrios Dendrinos asks whether an ancient Meter could have been in use there, and the Meter value as dictated by the suggested geometry formula would be 3.289868134.
That’s when I began to take the question of an ancient meter more seriously again.
3.289868134 has been referred to before as the “Third Meter” before, not only because it was the third candidate meter to be taken more seriously, but the name is also appropriate because One Third x (Pi^2) = 3.289868134.
This is also (Pi / 3) x Pi, and given as fond of (Pi/3) as ancient American mathematician seems to have been of (Pi / 3), perhaps at Tikal especially, they may therefore have looked favorably on the idea of 3.289868134 ft as a meter.
I have probably mentioned previously that the archaeologist and explorer Auguste le Plongeon contended that ancient Americans used the Metric System, although personally I found him difficult to take seriously because of the seemingly fanciful nature of some his published works. As absurd as this may sound to some, later less fanciful scholars have made the same contention, only more convincingly and with reference to historical sources (see Tlalcuahuitl).
I would happily agree with any of these sources, except that a problem that remains here is that I am very skeptical that ancient Americans used any single unit of measurement – the data from sources like George F. Andrews or even Teobert Maler simply does not seem to support this idea, very similar to how the overall data available on ancient Egyptian architecture simply does not support the idea of the ancient Egyptians having only measured in Royal Cubits.
What the data actually shows us seems simply too diverse for that, even though it may be enough to support the frequent use of some form of ancient Meter by either culture.
A possible Meter of 3.289868134 ft not only works to at least the 5th power with the inner diameter of the Stonehenge sarsen circle, it likewise works to at least the 5th power with Munck’s values for the Great Pyramid, which are herein presumed to be the Great Pyramid’s final measurements following the placement of a hypothetical layer of now completely missing pavement.
Likewise, it should be mentioned that 2 Meters of 3.289868134 ft = 6579.736269 / 1000 fr likely represents a probably ancient approximation of the Saros Cycle of 6585.3211 days. It’s a bit of a departure, but is roughly proportional to the departure represented by representing 18980 as 18997.72194, a gesture that finds some justification from certain likely ancient formulas, as has been mentioned on a number of occasions here.
Such things may also be facts of mathematical life given the structure of the numbers system itself, where the most common and most important fine ratio 1.000723277 is the ratio between the primary (A and B groups) sets of calendar numbers, for example 365.0200808 / 1.000723277 = 364.7562611 and etc. 6579.736269 x 1.000723277 = 6584.495241, which may be about the best representation of the 6585.3211 day Saros humanly possible given the particular building blocks available.
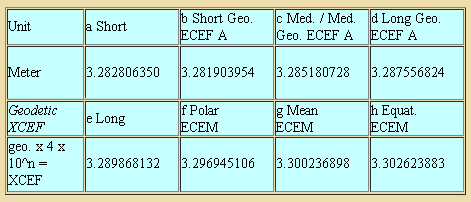
Awhile back I attempted to project a specrtum of unit values in a manner very similar to that of metrologist John Neal, which gave very pleasing results for the Meter and other units. For the Meter, at least four of the five strongest candidates are included
Projected values for an ancient Meter based on geodetic (measurement of the earth) schemes. This particular scheme manages to include both forms of the Indus Foot as a possible slightly larger meter consisting of 3 Indus Feet 3.300236898 ft and 3.302623883 ft (see also work by David Kenworthy).
However, the set of formulas seems to derange the possible 4 / 1.216733603 value, and a set of values this diverse is still something we should be hoping to avoid for most units if at all possible – not because ancient people were simple-minded when it comes to mathematics, but because we assume they weren’t gluttons for punishment either.
For good measure, I might add this from a post I posted elsewhere back in April of 2020
“The Aztecs, inheriting the vigesimal [base 20] counting system of the earlier Mesoamerican cultures, created a cadaster on which they recorded surveys of each family’s tract of land. The cadaster listed the distances measured by the surveyor for each tract. Their recording system consisted of maps that marked these distances by making a dot to record every 20 measuring units, called the “tlalcuahuitl,” which translates as “land rod” and which we will call “T”. For measures less than 20 T they marked the map with a vertical line, marking up to 19 of them, in groups of five. For measures less than one T they used a series of glyphs to represent fractions of T such as a heart [1/3 T], arrow [1/2 T], or hand [2/3 T]. But, what was the size of T, the basic Aztec measuring unit?
The native historian Fernando de Alva Ixtlilxochitl, writing about 1600 AD, described a vast Aztec communal dwelling built by the Tezcucan chieftain Nezahualcoyotl. This building was said to be capable of accommodating over two thousand people. Ixtlilxochitl writes: “These houses were in length from east to west four hundred and eleven and a half [native] measures, which reduced to our [Spanish] measures make twelve hundred and thirty-four and a half yards (varas), and in breadth, from north to south three hundred and twenty-six measures, which are nine hundred and seventy-eight yards.” 5 In his description, he spells out the basic “native” measuring unit for land, T, as exactly equal to 3 Spanish varas. So the question then becomes, how many feet are there in a vara? This is not an easy question to answer.
1234.5 varas = 411.5 “native measures”
https://www.academia.edu/37786698/The_Aztecs_and_the_Vara
I attempted some work with a vara of 2.788548009 = sqrt (7776 / 1000) ft, but I go to apply this and the magically suspicious number 1234.5 / 411.5 = another suspicious number 3, so whatever the Vara is, apparently the Aztecs were using the Spanish Vara before the Spaniards got there, or they had already adapted the Vara by the time this historical account took notice and “native measures” means simple multiples of the Vara?
Something that still may never have been considered is how close “411.5” is to the “textbook” value of the Full Moon Cycle, “411.78443029 days”, or that “1234.5 varas” = (2 / 1.620089105) x 10^n, very similar to 2 / 16.2 = 1.234567901, might herein with these considerations be overshadowed by the usual suspects, 2 / 1.622311470 and 2 / 1.618829140, had the quoted authors been aware of them.
I suppose on that note we might observe this for future reference as well – the Megalithic Foot value of 1.177245771 ft links a particular series. Correct decimal placement aside
2.012073535 = mean diameter sarsen circle / 50 = 60 Mystery Units of 1.676727943 ft
2.012073535 x 1.177245771 = 2.368705060 (possible Ubaid Cubit)
2.368705060 x 1.177245771 = 2.788548009
2.788548009 x 1.177245771 = 3.282806357
3.282806357 x 1.177245771 = 3.864669901
3.864669901 / 2 = 1.932334951 = “Cuicuilco Number”
Based on Emil Haury’s data for the Cuicuilco Pyramid, the metrological values of Royal Cubits and Hashimi Cubits may be present in the design;
206.2648062 (120 Royal Cubits) / 1.067438159 (Hashimi Cubit) = 1.93233495 x 10^n
1.93233495 is rather a strange number, but it does appear to be a metrological fact of life that we presume the ancients harnessed toward good use. Perhaps it’s only foggy memory, but I’m a little bit surprised to see here how it can be generated from both 1.177245771 and 1.067438159. Perhaps it it’s more important than its getting credit for.
So that is the state of an ancient Meter as it remains – it’s something that’s very possible, yet the specifics of it remain seemingly difficult to sort out entirely. The ancient Meter has great potential for being actual historical truth, yet it seems to remain a perennial metrological problem child.
Maybe someday a definite link to other units will be found and recognized which will settle the matter once and for all. Maybe 2021 will be the year.
Cheers and Happy New Year!
–Luke Piwalker