Progress in Metrology: The Eclipse Year Unit Classified

It almost tried to get past me, but thankfully it kept bothering me until I went back and took another look. A study inspired by DUNE at GHMB resulted in identifying a chain of numbers linked by 2 Pi that included both the Lunar Year AND the Eclipse Year, and today I went back and tried to take another look at it to be sure.

An incomplete rendering of the series based on the important number 1115.419204 which may have already been found at least several times in ancient American architecture. It is proposed to be included in the base footprint of the Pyramid of Niches, and may be a pyramid diagonal length at Tikal if Maler’s data on the exteriors of the Temple Pyramids, which were generally in rather rough shape at the time, can be accepted.

1115.419204 may also appear in the El Castillo Pyramid at Chichen Itza. The number has more than one geodetic property, although I’m omitting discussion of those here but some details are included in the GHMB post linked above.

Of metrological significance,

“Circumference (1115.419204 / 2 Pi^1) = Diameter 177.5244799 / 2 = Radius 88.76223994 = Lunar Leap Month x 3?
(1115.419204 / 2 Pi^2) = (1 / Lunar Year) x 10^n
(1115.419204 / 2 Pi^3) = Venus Orbital Period x 2
(1115.419204 / 2 Pi^7) = 1 / Eclipse Year”

While we may not (?) be able to comfortably identify the unit historically, a unit that is fundamental to the “Best Eclipse Year” turns out to be 2 Pi away from the Incidental Megalithic Yard, which was currently thought the limit in the expansion of a metrological unit series in 2 different directions from the Sacred Cubit.

The 2 Pi metrological series and what were previously thought to be its limits.

I have recently commented on this remarkable ability of the Sacred Cubit to host a series in either direction,

“I’m quite taken with how if you divide a Royal Cubit by a Remen, you get the amazing Megalithic Foot, one of two numbers that ancients seem to try to build into everything regardless of geography so far; if you multiply a Royal Cubit by a Remen, you get the amazing Sacred Cubit.

That much more reason for them (the Ancient Egyptians and others) to have been so stuck on the Royal Cubit and Remen, if you ask me.”

The revised series now featuring the “Eclipse Unit”.

So what we see is that even though the “Eclipse Unit” has been a rather mysterious metrological oddity because it refuses to resolve into other known units, the reason for that is apparently that it is a unit in its own right, and very closely related to most of the metrology being observed though the very same series.

This and the ability to form the “Eclipse Unit” from other metrological units (AE Megalithic Yard / Megalithic Foot x 15 = Eclipse Unit, Hashimi Cubit squared x Remen / 4 = Eclipse Unit) lend a strong sense of legitimacy to the particular unit value.

Thus we can relate the “Eclipse Unit” to other units in both of the ways identified here as best because they are exact

I still don’t know exactly what to think of the unit as – a “Eclipse Year Unit”? An “Eclipse Unit”, as David Kenworthy thinks of a similar unit value? A “Nilometer Cubit”? Perhaps its technically nothing to do with a Cubit – but we do now know more than ever that it is something, and that it is a metrological unit that belongs with the others.

Perhaps the next thing that might happen is to go back to the chambers and coffers of the Giza pyramids; awhile back I wondered out loud here what if the mystery measure of the Giza coffers and the mystery of the Nilometer Cubit were one in the same, but I haven’t actually answered the question yet. Maybe now we have more context and more confidence to facilitate that very thing.

The Eclipse Year Unit may not have been firmly identified, but it has now been certainly classified so that we can see where it fits into the scheme of things, which also means that multiple pointers point to it as legitimate.

It doesn’t seem like long ago the Hashimi Cubit (aka Pied du Roi) was going through the very same process.

I decided that before I posted this, I would briefly check and see if there is anything recognizable or worthwhile beyond the Eclipse Year Unit in the series, and in fact there is. Another 2 Pi out from the Eclipse Year, we find the Anomalistic Month value, as we seem to have recently displayed in one of the Mayan “altars”.

Since it registers this way as a value with a seemingly unique base unit, we presume such a unit would be required for the expression of the standard Anomalistic Month value; thus it may require christening to the effect of the “The Anomalistic Month Unit”.

The diagram now looks like this

So, we now have a total of nine ancient units of measure directly linked in series by 2 Pi, plus we have what appears to be a total of 5 units based on and linked by Pi^n.

The currently known metrological unit values based on a valid whole number and Pi^n.

Thankfully, we now seem to know more about these units and the corresponding astronomical values they embody, and how to get from one to the other using 2 Pi.

The calendar stone from Ucanal with a projected radius of 27.55182815 / 10 ft, especially being a circle “calling for” 2 Pi, is presumably able to communicate a rather wide range of astronomical constants from a single series, as would be the other calendar stones by the same account.

This is of course not limited to ancient American calendar stones, it no doubt also applies to ancient architecture elsewhere.

Consider this observation: 360 / 27.55182815 = Sunhoney Number / 2.

The Anomalistic Month Unit or its equivalent would seemingly be also required to metrologically define the suggested measurement values for the Sunhoney Stone Circle, so we can already point to what may be at least one example of the Anomalistic Month Unit in actual use in Megalithic design.

–Luke Piwalker

 

A Little More About Mayan Calendar Stones: Ucanal

To be honest, recent work has already uncovered so much that is new, it may take some time for all of it to really sink in. I’m really only still starting to learn why the ancient Maya combined some of the numbers in their altars that they did.

In my most recent notes there is a description of a presumably circular altar at Ucanal in Guatemala, from Vol 2 of Sylvanus Morley’s The Inscriptions of Peten, page 196. The altar is associated with Stela 3

As described by Morley,

The basic proportions and measures in feet are 

D 1.68 = 5.511811024 C = 1.731586591 R = 2.755905512 T .53 m = 1.738845144 D/T = 3.169811321 C/T = 1 / 1.0004191620

 

Some might wish to interpret that as meaning the thickness was simply equal to the radius, but we may wish to check if something more subtle might have been at work.

 

The radius of course looks rather like the Anomalistic Month of ~27.55 days; the optimum value for the Anomalistic Month is currently thought to be (27.19256444 x 10) / (Pi^2) = 27.55182815 days. That might well have happened here, both because it’s not far from 27.55182815 to the Best Eclipse Year, however surprising. 27.55182815 x 4 Pi = 12 / Best Eclipse Year.

 

17.311322418 x Pi^n produces a brief, humble series. 17.311322418 is the short version of the Solar Calendar Year / Palestinian Cubit. It’s 2 / 1.1553132490 = Tzolkin 259.75757575 / Venus Orbital Period 224.8373808, and we can built it out of Megalithic Yard and Megalithic Foot: (2.720174976 / 1.177245771) / 2 = 1.155313123.

 

On the whole, though, the calendar stones may be more mathematically interconnected than it might appear at first sight. The scheme suggested here for the original proportions of this Ucanal “altar” might be something of a departure from the Sun Stone and Yaxchilan designs, and yet perhaps not necessarily a great departure.

 

It has been suggested for some time by my work that the number (30 / (Pi^2)) may have been highly conducive to the workings of more advanced Mayan calendar systems which may have been documented through architectural or artifact design itself rather than in more conventional ways such as texts or inscriptions, even though the significance of the structural equations themselves may be supported by the associated inscriptions.

 

Sadly, in this case, at least from Morley’s description, we might have difficulty finding out whether what the measurements show us match what the inscriptions show us, but this still seems a worthy study because the data implying a direct expression of the Anomalistic Month of ~27.55 days may be without precedent.

 

If nothing else, it may be a good reminder that a variety of Megalithic Yards are proposed to exist on account of this work, and that this may ultimately reflect the ancient desire to represent or record a number of Lunar Cycle values that are equally similar yet diverse, i.e., Anomalistic Month, Sidereal or Tropical Month, and Draconic Month, because again, we can readily construct the elusive and capricious figure of (27.19256444 x 10) / (Pi^2) = 27.55182815 from the “Incidental Megalithic Yard” of 2.719256444 ft.

 

Besides 1.0823232323 and (30 / (Pi^2)) = 3.039635509, one of the other numbers that is trying to become emblematic of ancient American calendar stones is the diameter of the Sun Stone itself, circumference 11.77245771 ft / Pi = diameter 3.747289670

 

Perhaps not that surprisingly, we find that 3.039635509 and 3.747289670 does seem to be interactive with a proposed value for the Ucanal “altar” of Radius 27.55182815 / 10 ft, and there is apparently exponential value present as well. 

 

At all the way 27.55182815 / (3.747289670^5), we are still looking at valid data in the form of the seldom mentioned number 3.728757071, which was Carl Munck’s “Grid Point” for Marcahuasi, Peru’s “Monument to Humanity”, which fact will bear witness to the number having at least a modicum of both resonance and relevance. At the very least, 3.728757071 will form a significant series with 1.177245771 (which makes it directly accessible from the Great Pyramid’s missing apex section statistics), and it will essentially form the makings of the Best Eclipse Year if exposed to the powerful data mining tool, sqrt 60 – rather directly:

 

3.728757071 x sqrt 60 = Best Eclipse Year / 12

 

We can also squeeze this number out of the Great Pyramid using Munck’s base perimeter and our second favorite Phi approximation, 1.6188239140.

 

It may not be the most useful number, but it is something, and I do suspect it has still unappreciated significance to ancient American calendar systems, one example being that it can link the A version of the Calendar Round directly to the reciprocal of 12 times the perimeter of the Aztec Sun Stone, which is seen in Egypt as Royal Cubit / Remen = 1.2 Megalithic Feet, whereas Royal Cubit x Remen = Sacred Cubit and diagonal to Royal Cubit and Remen = Palestinian Cubit.

 

3.728757071 and (30 / (Pi^2)) = 3.039635509 interact in a way that affords exponential use of 3.039635509 to form a series that includes important numbers like (Pi / 3) and the reciprocal of Pi.

 

The way that 27.55182815 and (30 / (Pi^2)) = 3.039635509 interact is probably even more interesting. Among the numbers that are recovered that way are what is presumed to be one of several valid thickness figures for the Aztec Sun Stone that seem to result from the rough-hewn bottom of the artifact not giving a consistent thickness value, apparently giving different thicknesses from different sources even though their circumference values are essentially consistent to within approximately a few tenths of an inch.

 

10.823232323, which is quickly trying to become emblematic of these altars, actually works with 27.55182815 to at least the second power. The circumference would be 17.311322418 ft which is 6 / Best Eclipse Year.

 

17.311322418 x Pi^n produces a brief, humble series. 17.311322418 is the short version of the Solar Calendar Year / Palestinian Cubit. It’s 2 / 1.1553132490 = Tzolkin 259.75757575 / Venus Orbital Period 224.8373808, and we can built it out of Megalithic Yard and Megalithic Foot: (2.720174976 / 1.177245771) / 2 = 1.155313123.

 

1.1553132490 / 1.0823232323 = 1.067438159 and 1.067438159 / 1.0823232323 = 1 / long Greek Foot (in “modern” feet).

It is always noteworthy to find what may be 1.067438159. The number seems to have been highly favored, and for many reasons.

Let’s step back for a moment and touch base with the original data projections and see what else we might find.

 

D 1.68 = 5.511811024 C = 17.31586591 R = 2.755905512 T .53 m = 1.738845144 D/T = 3.169811321 C/T = 1 / 1.004191620, with D, C, and R
(diameter, circumference, and radius) possibly meaning D 5.510365631 ft, C 17.31132418 ft, R = 2.755182815 ft.

 

1.738845144 might be where they are trying to let the Metonic Cycle into the picture along with the Eclipse Year, or it could one of several other important numbers just above that range. For the diameter/thickness (D/T) ratio projection of 3.169811321, I’m reminded of 3.176266261, which I’ve been saying for some time seems to be an important number in ancient astronomical math, that I’ve reported seemingly finding at both Tikal and in its immediate vicinity.

 

Numbers in the range of 1.0004191620 very often turn out to be 1.006036766. It hardly seems by chance that the mean diameter of the Stonehenge sarcen circle projects as 100.6036766 ft.

 

This would make the thickness of the stone to be circumference 17.311322418 ft x ( 1 / 1.006036766) = 1.741582860 ft, which would be one of the two most expected figures for the exact meaning of 1.74 ft or greater (the other one is 1 / Radian 57.29577951 = 1.745329252 / 10^n). It is twice the height calculated for the outer door of Tikal Temple II, divided by 10:

 

width 7.396853331 (one Squared Munck Megalithic Yard) ft x (ht/width ratio 1.177245771) = height 8.707914303 = 17.41582861 / 2.

 

A possible problem with this might be that the product of the diameter and the thickness might then become a nonsensical figure? – not that we have been able to establish protocols that the diameter or radius or circumference times the thickness is always supposed to give a meaningful result, but perhaps other possible scenarios deserve equal attention.

 

Even more strangely, putting the reciprocal of the Radian into that scenario may also produce ostensibly nonsensical figures, it appears.

 

However the combination of 3.176266261 with 17.31132418 might also prove to be something that the designer actually wished to communicate? I think it’s best seen if we switch around larger and smaller here: 3.176266261 / 17.31132418 = 18.34791047 / 10^n. 18.34791047 / 2 = 9.173955233, which has already becomes something of an apparent trend in Mayan altar proportions, with some justification for that already having been given.

 

There is another number (at least one) in the 1.74 range, and I very recently wrote a post in “lament” for it even though it may in fact be beginning to stage a revival. 

 

That is the number we get if we apply 3.176266261 as the projected ratio, and if we do so, then the circumference/thickness ratio becomes one of the next most likely fine ratios implied after 1.006036766 for the meaning of C/T = 1 / 1.0004191620, which if we are not too preoccupied with exactitude, is 1.002151140.

 

Note that this gesture ushers in the Synodic Period of Jupiter to accompany the indications of Jupiter and Saturn that may already be present.

 

What may have just happened is that once again, 3.176266261 may have exhibited its usefulness as a number significant to calendar functions, and in doing so, may have facilitated access of further data pertaining to both the Jupiter Synodic Period, and the Metonic Cycle (because that is in the context of the post about the Chephren pyramid’s “Grid Point”).

 

If this inquiry has managed to consistently follow consistent logic then, the raw data

 

D 1.68 = 5.511811024 C = 17.31586591 R = 2.755905512 T .53 m = 1.738845144 D/T = 3.169811321 C/T = 1 / 1.004191620

 

Would refer to refined figures of 

 

D 5.510365631 ft, C 17.31132418 ft, R = 2.755182815 ft T = 1.734856330 ft
D/T = 3.176266262 C/T = 1 / 1.002151140 = Saturn Synodic Period 399.1413901 days / 400.

 

While it would be imprudent to insist this in any way because of my knowing so little in general here, it may well be possible that if there were correspondence between the measures, and the decorations and conventional chronology, that like the altars at Tikal, this stela / altar pair may have commemorated the ending of a cycle coinciding with the end of the dual retrograde of Jupiter and Saturn.

 

Exactly why there would be strong overtones of the Anomalistic Month and the Metonic Cycle as well as the Eclipse Year, I probably couldn’t say – was the Metonic Cycle the large cycle here, or one of them? – but suffice it that

 

a) the basics of an actual working model for the stone have been identified

 

b) that we seems to see looks rather skillful and not that unfamiliar all things considered

 

c) the ability to recover even that much astronomical data from the stone’s design seems to reinforce the premise that it is indeed a calendar stone even if a somewhat unusual one.

 

Note that as I continue to try to further advance the idea that a theme of bondage or captivity in the altar scenes may refer euphemistically to the standstill or retrograde of celestial bodies, that the drawing of altar 3 at the link toggles via a slider to also show a photograph (if you click on the drawing), wherein the theme of bondage can clearly be seen, as in this detail from the image which seems to show a seated figure with arms behind back and ropes around arms.

 

If we are fortunate then, today we have further advanced our understanding of the calendar stones by at least a little, and maybe even got to experience a little bit of what it must have been like to be Maler or Morley rediscovering some of these things.
–Luke Piwalker
 

I Survived Mayan Altars (I Think)

I’ve been revisiting some of the original passages from Teobert Maler and Sylvanus Morley giving dimensions for Mayan circular “altars”, or as I prefer to think of them, calendar stones or calendar calculators. The Aztec Sun Stone came along early in my newly found devotion to applying Munck’s numbers to the mystery of ancient monument proportions as they concern astronomy, and I drew tremendous encouragement at that time from the way the Sun Stone works as a calculator, and in fact I still do.

I’m not seeking to solve all of them, and in fact I think in the latest round I may have come closer to that than I ever would have expected, but I was hoping to learn more about their nature and character, and I think I may have.

A perhaps surprising number of ancient Mayan “altars” may, when it comes to their diameters, be based on the same basic metrological concepts as the Sun Stone. At the very least, two others can quite probably be considered scale models of the Sun Stone in terms of radius, diameter, and circumference. This in addition to Yaxchilan being able to boast one circular stone that seems to imitate the Sun Stone directly in terms of diameter, and perhaps another whose thickness may imitate the Sun Stone’s circumference, and so forth.

That may be the single biggest trend I see running through the data, the possibility of proportions “recycled” from one example to the next, or especially of a significant number of examples having diameters that would seem to be based on the very same unit of measure as the Sun Stone.

Although there seems to be more to learn, I think that the latest round has also taught us some valuable lessons about how Jupiter and Saturn’s cycles can be included in the calculations that may already involve Solar, Lunar and Venus cycles.

The Yaxchilan version of the Sun Stone (S39 A4) is interesting. Just recently we looked at this “altar” but I don’t know if all of its secrets have been deduced yet.

As with the Sun Stone, the radius, diameter and circumference are thought to be Radius 1.873644837 ft, Diameter 3.747289674, Circumference 11.77245771 ft.

However, the thickness of the stone at Yaxchilan is different from the Sun Stone. It’s given as .33 m = 1.082677165 ft, which we might quite easily assume to be the 1.0823232323 Jupiter Orbital Period fraction that has been seen recurring in numerous Mayan “altars” – a prime example of “recycling” numbers from one artifact to to the next.

The circumference / thickness ratio would be 11.77245771 / 1.0823232323 = 1.087702579. It’s likely to take more thought to better understand why we would see this number in the proceedings in spite of a risk of confusion with 1.082323232, when it may be unusual for 1.087702579 to appear anywhere in such a direct form.

Speculatively, we’re seeing it because it’s 4 times the “IMY” version of the Megalithic Yard of 2.719256444 ft, so it may be the IMY we’re really seeing. The “IMY” can be considered as a primary form of the Draconic Month, and further simple division of the “IMY” may result in a valid form of the Nodal Cycle at

(2.719256444 x 10^n) / 4 = 6798.141118 / 10^n.

Because 6798.141118 / 1.000723277 = 6793.227733, much closer to the target value of 6793 days, these two could constitute a primary pair of approximations. Still, it isn’t entirely certain because there are some mathematical root maneuvers that seem to apply to some of the larger Lunar Cycles and the correct way to classify them may remain unknown. For the Nodal Cycle, the cube of 1.5 “AEMY” Megalithic Yards could be valid if afforded a distinctive set of alternate approximations:

(2.720174976 x 1.5)^3 = 6793.042009 / 100

Things are similar for the Saros Cycle, we have a perfectly good primary pair and yet using 5 / (Pi^2) as the fourth root of the Saros produces another approximation that’s hard to argue with

(5 / (Pi^2))^4 = 6586.89940 / 10^n, which is readily accessed more accurate than one of the proposed primary pair. More important, we may have already encountered situations in design that have actually indicated this number, and more (5 / (Pi^2)) is of course very directly related to the (30 / (Pi^2)) figure that has already been rather prominent in the proceedings on calendar stones.

In the case of another large lunar cycle, the Metonic Cycle, there is also a similar type of approximation – the cube of the reciprocal of 2 Remens, which may actually be working as a primary value.

Just for the record then, some aspects of the calculator function of the “altars” may not yet be quite understood because of some of the cycles they may calculate may not yet quite be understood. Exactly what they did about the larger Lunar Cycles is still still potentially puzzling.

One of the calculator functions of Yaxchilan’s version of the Sun Stone may be

Circumference 11.77245771 x Thickness 1.0823232323 = 12.74160448.

This would be (Lunar Year x 360) / 10^n and (9.173955226 / 2) / 360, with also 9.173955226 looking like something that is trending in the circular “altar” stones as mentioned in some of the immediately preceding posts.

12.74160448 is part of an output series driven by 1.622311470^n that may help to clarify the role of the so-called “Stecchini Cubit” or “Lepsius Cubit” in astronomical calculations. One of the more distinguished aliases of 12.74160448 might be (sqrt 60) x (Pi^2). 2 Pi can retrieve data from the number 12.74160448 that is often associated with Stonehenge (see sarsen circle mean value) and data that has been associated with the Sun Stone (12.74160448 / ((2 Pi)^2)).

It may have been accepted in part because it may enjoy relatively high reactivity with the standard approximation of the Saturn Orbital Period.

Interestingly, the resultant series from combining 12.74160448 with the Saturn Orbital Period includes 1.370778380 = (1 / 72) x (Pi^2), a number I have not seen in ages and now suddenly it appears in one of the “altars” promising to be an important missing link in several astronomy calculations. The series also includes the Indus Foot value and 12 x (Pi^2), which has established itself as the vital link between Half Venus Cycle and Venus Orbital Period.

While it was quite important to Michael Morton’s work, one of the few places I can think of seeing 1.370778380 in actual situations is that for 20 years, it turns up every time I go to inquire about the height at which the Great Pyramid’s passage met with its surface slope.

This prior occurrence would have been at Piedras Negras (Morley, –Peten Vol 3, pg 285), where Morley gives dimensions of D 2.16 = 7.086614173 and T .42 = 1.377952756, which I suspect means 1.370778380. The circumference / thickness ratio would be (2.16 Pi) / .42 = 1.615676222 and while it’s not impossible that this could mean Apsidal Cycle / 2 / 10^n = 3233 / 2 / 10^n = 1.6165, the more sensible complement may be 1.622311470 — “one of those numbers they were trying to build into everything”.

Is it actually advantageous to combine 1.370778389 with 1.622311470? Well…

1.370778389 x (1.622311470^1) = 22.23829503 for the Circumference, 22.23829503 / Pi = 7.078669161 (1 / 12 Megalithic Feet) for the Diameter, and 7.078669161 / 2 = 353.9334581 / 100 again for the Radius
1.370778389 x (1.622311470^2) = 3.607744171 – meaningful number, see recent speculation on Waun Mawn and Stonehenge
1.370778389 x (1.622311470^3) = 585.22884651 / 10^n – Long Form of Venus Synodic Period?
1.370778389 x (1.622311470^4) = 18990.40380 / 2 / 10^n Calendar Round C value / 2 / 10^n

It seems to be, since we obtain 5 / Venus Orbital Period, the “Dresden Version” of the Venus Synodic Period, the standard Lunar Year, and the Half Venus Cycle from the combination of the two. That’s a good supply of astronomical data recovered from just two numbers.

Thus 1.370778389 may be a lost missing link between calendar formulas.

In fact, even before this post has reached completion, it is observed that 5 / 1.370778389 = 364.7562635 / 10^n. 1.370778389 is a backhanded simple fraction of the A version of the Solar Calendar Year. Although 365.0200808 is often preferred and probably somewhat more functional as an approximation of the 365 day calendar year, it’s thought that Teobert Maler’s data for the El Castillo Pyramid at Chichen Itza conveys the use of (Pi / 6) as the square root of the A version of the Solar Calendar year, at the same time as suggesting (Pi x 6) as a valid square root of a Lunar Leap Year.

12.74160448 probably has other value to astronomy that hasn’t begun to be considered here yet, including that it can link Jupiter’s Orbital Period to (Best Eclipse Year / (2 Pi)), and Jupiter’s possible main Synodic Period value to 360 / Lunar Year.

I almost get the feeling we’ve recently encountered 12.74160448 before in slightly different guise, but I can’t account for that at the moment except that 25 / 12.74160448 = 1.962076286 which I’ve been saying for a few years now seems to have been an important number to the Mayan astronomers and architects.

Some trends in the altars may remain somewhat mysterious for while longer. I suggested in a previous post that one may measure 1.838737943 feet and that “1.838737943 is probably a new Wonder Number”, and the possible role of the number 1.834791046 in ancient “altars” including additional examples at Yaxchilan still probably hasn’t been fairly considered, for example.

On the other hand, as many as a dozen of these calendar stones or calendar calculators may have been solved now. There’s one at Uaxactun (data Morley, -Peten, Vol 1, pg 226) associated with Stela 12 that is made of such classic ingredients that it pretty much solves itself, as diameter D .75 m = 2.460629921 ft and thickness T .46 m = 1.509186352 ft being rather obviously D = 2.465617776 ft and T = 1.519817755 ft respectively.

It much resembles some of the ancient American circular architecture we’ve looked at, where referring to Marcello Ranieri’s data projections especially, we saw a number of examples that look the architects are quite enthusiastic to express 1.622311470, one of those two numbers that it seems they wanted to build into the design of everything, in its form of 2 / 1.622311470 where it is one of the two most powerful data retrieval tools ever discovered.

2 / 1.622311470 = 1.232808888 = D = 2.465617776 ft / 2

Even without looking at the calculator functions, this generates such a harmonious package that we can probably safely appraise it simply on the basis of the “strength of the numbers”. (The same approach was used with the Sun Stone; it wasn’t until later that it was realized some of the voluminous data it contained).

It almost goes without saying, but the presence of the Venus Orbital Period, often rather directly, may also be a trend of the altars, and again, the Sun Stone’s radius and diameter are also directly linked to the VOP, a trait that will be shared with other stones that are scale models of the Sun Stone in terms of diameter.

One altar at Uaxactun of D 1.37 m = 4.494750656 ft = 2.247375328 / 2 ft = ~2.248373808 (Morley, -Peten Vol 1, pg 167); the altar associated with Stela 1 at Xultun (Morley, -Peten Vol 1, p 413) Radius 2.19816273 ft = ~500 / 224.8373808 = 2.223829499 ft; Piedras Negras (same specimen where we may have found 1.370778389 earlier in this post) circumference 22.26325503 = ~2.223829499 ft; these may all be examples of relatively straightforward expression of the Venus Orbital Period using measurement.

There may be something of a trend toward toward a measure of 1.60 m = 5.249343832 recurring. It’s not entirely certain but one possible meaning is that this intended 1/2 of (Pi / 3) x 10 = 5.235987756 ft = 1.59592 m, since (Pi / 3) is so essential to many vital exponential series just as it was at Tikal when (Pi / 3) was found to be what is apparently a vastly important key to the mathematics in use there. Very little there made sense until (Pi / 3) was brought in, and then suddenly most of it made sense.

Earlier on, I suggested that perhaps (Pi / 3) should be considered as Tikal’s “site constant” just as Munck maintained that the Radian was Giza’s “site constant”, but I’ve begun to have concerns that doing so might contribute to a false sense that the applicability of (Pi / 3) should be thought of as limited to Tikal when in fact it may be highly applicable throughout the mathematics of the ancient Americas.

There are even several calendar stone specimens wherein the Half Venus Cycle could be spelled out directly; the circumference of “Altar 3” at Altar de Sacrificios or of the altar associated with Stela 1 at Uaxactun come to mind although it remains to be seen for certain.

I’m also attempting to give fresh consideration to the “Disco de Chalco” even though I have two slightly conflicting datasets (D 102.5 m T .20 m and D 103.0 m T .23 m) for it.

My guess is that this circular stone too may be cut from the same cloth as the Aztec Sun Stone, as a 9:10 scale model in fact, in terms of diameter.

I suspect that the intended interpretation of the diameter then was 3.372560706 ft (~1.028 m; mean of 102.5 cm + 103.0 cm = 1.0275 m).

Using a combination of pixel measurements and calculations on a photograph of the Disco de Chalco suggests that the diameter of the inner circle may be ((1 / (Pi / 3)) / 2 = .4774648293 ft, and notably also that the largest circle except for the outer diameter of the disc itself has a diameter of 2 Egyptian Remens. This then gives the square of 1.177245771 as the ratio between the diameter of this circle that encloses a circle of 28 dots, and the outer diameter of the whole disc.

It’s not certain what all this means, but 1.177245771^2 does have some significance and a measure of 4.774648293 seems plausible at Tikal, as we have seen in recent work on architecture there.

That’s maybe enough for the moment – it may be all the information I actually have for the moment, but having recently proposed that some of the decorations of ancient American stelae and altars might not be meant to be taken too literally, I was surprised to see these remarks when looking something up in Wikipedia’s article on Piedras Negras.

“Panel 12 of Piedras Negras shows three neighboring rulers as captives of Ruler C. One of the captives might be the ninth king of Yaxchilan, Joy B’alam (also known as Knot-Eye Jaguar I), who continued to reign after the panel was made. As subservient rulers were often depicted as bound captives even while continuing to rule their own kingdoms, the panel suggests that Piedras Negras may have established its authority over the middle Usumacinta drainage in about 9.4.0.0.0 (514 AD).[6][7]“

I will again ask whether such “decorations” actually depict scenes of ritual sacrifice of important captives from neighboring cities, or whether they may be euphemistically or symbolically describing at least in part the behavior of the planets rather than the behavior of the royal populace.

–Luke Piwalker

 

 

 

Where Chephren Once Stood

I thought I’d stare a bit more at my expanded tables of ancient American “altar” data and see if any more helpful patterns appeared to coalesce.

I may have spotted one, but it may bring up something of a strange and sad tale.

There is a number we hear from very little these days, which is unfortunate, because it’s an amazing number. It was Carl Munck’s “Grid Point” for the Great Pyramid in his “geomathematical” coordinate system, with the full coordinates being Grid Latitude 67858.40132 / Grid Longitude 11.77245771 = Grid Point 5764.166072.

I more or less still remember that number even when I’ve barely put it into a calculator in 12 years, I referred back to it so often. Every new find, every new number, was referred back to the purported “Grid Coordinates” of Giza’s major pyramids.

For the record, the number is still alive and well at Giza. How so? Well for starters,

5764.166072 x 2 = 1.152833215 x 10 – the Egyptian Royal Foot in “modern” feet (which are apparently the ancient reference unit of measurement that gives such amazing values to other ancient units of length).

Remen in inches times (2 Pi) squared = 1.216733603 x 12 x (2 Pi)^2 = 5764.166072

For whatever it may or may not imply (some may associate the number 5760 with calendar systems already), we can construct it as 5760 x 1.000723277.

5764.166072 may be safely preserved by the Great Pyramid, in any number of ways.

As a token of proof, the most obvious way to do it might be to simply convert Munck’s height for the Great Pyramid, part of his non-“geomathematical” work that we are still striving to conserve, in inches

Munck Height Great Pyramid 480.3471728 ft x 12 = 5764.166072 inches.

There’s something that doesn’t get mentioned often enough, that’s probably a first for this blog.

What’s sad is that we may have been barking up the wrong tree totally with the “geomathematical” considerations, and what’s strange is still how little of this number I see in actual practice, even for just having identified it as such a simple variation on the Egyptian Royal Foot.

I actually brought it up neither to lament nor to reminisce, but because it managed to turn up in a train of thought about the Mayan calendar stones that I think is rather interesting.

It’s the one where the math we use around here doesn’t necessarily share a protocol with the “common” calendar math when it comes to the relationship between Eclipse Year, Jupiter Orbital Period, and Metonic Cycle, not that there was necessarily a common tactic that worked.

The gist of it is that Metonic Cycle / 2 = ~Eclipse Year x 10 and Eclipse Year / 8 = ~Jupiter Orbital Period / 10^n, but the math I am using seems to be able to distinguish the ideal Eclipse Year from the ideal Metonic Cycle instead of lumping them together along a 2^n chain like that.

Thus far the ideal Metonic Cycle seems to be the cube of the reciprocal of 2 Remens x 10^n: (1 / (1.216733603 x 2))^3 x 10^n = 6939.425316.

That’s where we get the distinction between Eclipse Year and Metonic, since

6939.425316 / 2 = 346.9712658

Which isn’t registering as an Eclipse Year since there are better things we can use, and doesn’t seem to divide via 2^n into a Jupiter Orbital Period figure that is useful to us either.

At any rate, this discussion manages to dredge up the subject of the Chephren Pyramid’s “Grid Point” of 5764.166072, simply because

40 / 6.939425316 = 5.764166072

Thus in the course of the inquiry we learn a new thing – that 8 / Egyptian Royal Foot = 6.939425316 = 1/1000th of what may well be the ideal figure for the Metonic Cycle.

One other thing that might be worth mentioning here, 30 / 5.764166072 = 5.204568990, which is also of relevance to calendars because that is likely one of the premiere approximations of the number 52, as in 52 weeks in a year or 52 years in a Calendar Round, etc.

We should probably be allowed to feel entitled to take liberties with that if only because it isn’t precise in the first place. There aren’t really “52” weeks in a year, 52 weeks x 7 days = 364 days, not 365.

5.204568990 is half of 10.40913798, which we can easily obtain from Pi / Munck’s Perimeter for the Great Pyramid (i.e., measured from proposed pavement level): Pi / GP Perimeter 3018.110298 = 1.040913798 / 10^n.

1.040913798 was influential in working out how the ancients would have preferred to represent the Equatorial Circumference in Miles, and how the consensus symbolic Precession Cycle value of 25920 (years) can be involved

25920 / 1.040913798 = 24901.19742 miles (textbook figure for the Equatorial Circumference in miles = ~24901.55 miles).

Not to be outdone, 5.764166072 x 43200 = 24901.19742

That’s the actual story of the number. Munck and Morton should get all of the credit for that, but as it happened, Munck envisioned the equation, Michael Morton perfected it, and I solved it and then eventually explained why we probably had the right solution. By the time I knew this number had a valid cube root of 24 Remens, I knew we really had something.

As of the most recent effort on the Stonehenge lintel circle, my model gives the maximum circumference as 104.0913798 feet, which has been discussed in various posts referring to Stonehenge (it didn’t get there just because it’s an interesting number found in the Great Pyramid, it’s dictated by a much more detailed list of considerations).

The other reason I wanted to bring all this up in the first place is because of something else back where we started.

A subject in question is one the Jimbal Altars (J.1) from Guatemala (data source: Tikal Reports 33). The diameter is rated as Diam 1.06 m = 3.477690289 ft, so we get to ask, does this mean the ideal Eclipse Year value 346.5939351 / 10^n, or does it mean half of the seemingly ideal Metonic Cycle 3469.712661 = 6939.25316 / 2?

Interestingly, as a diameter, 3.465939351 may prove to be associated with a somewhat awkward circumference value, while as a diameter, 3.469712661 would be associated with a circumference of diameter 3.469712661 x Pi = circumference 10.90042380, which I find very interesting because in the preceding post, it was discussed how the reciprocal of this number provides the necessary linkage between the Saturn Synodic Period and what may well be multiple Lunar Cycles

“Saturn Synodic Period 377.8016633 / 9.173955233 = 411.8198244 thus far the preferred form of the Full Moon Cycle of “411.78443029” days, and

Saturn Synodic Period 377.8016633 x 9.173955233 = 346.5935546 thus far the preferred form of the Eclipse Year of ~346.62 days”

1 / 9.173955233 = 10.90042380

So what have been happening is that they were choosing scenarios that actually accommodate both the Eclipse Year and half the Metonic Cycle even when they have technically become distinctive things. A lack of an applicable 2^n series to tie together the Eclipse Year, Jupiter Orbital Period and Half Metonic Cycle really doesn’t so far seem to have been an obstacle to them, and if there is therefore such a trend of finding 9.173955233 in altars, then the Jimbal altar under discussion may have a circumference of 10.90042380 as another example of the same.

Analysis of the calendar stones is still a science in its infancy, so I’m still rather proud of any “baby steps” that might be taking place with it.

–Luke Piwalker

Some Surprising Properties of Calendar Stone Numbers

I’m continuing to try to round up further data on ancient American “altars” – or calendar stones as I prefer to think of them. I’m perhaps a bit too busy trying to think of them as advanced calculators for intricate calendar cycles to think of them as “altars”, but obviously in spite of any myths commemorating the exploits of the planets, the ancients knew the cycles of the planets well enough to know they had the predictability of inanimate objects, which is probably enough to make them more the ancient version of NASA much more than it is something that earmarks them as any kind of cult.

Finding (and organizing) data is often a time consuming and relatively unrewarding process, that can exclude being able to get deeper into the mathematical work, but I am quite intrigued with the subject once again, especially since a review of the data gathered thus far suggests a possible pattern of relationships between many of these “altars” and classic examples of their kind such as the Aztec Sun Stone or Tizoc Stone.

If there is very much overlap between their measurement values, it may make our job understanding them much easier.

When pointing out the occurrence of one of the Sun Stone numbers in the design of Hadrian’s Library recently, I had the occasion to mention how generally rare it’s been to encounter some of these numbers, even in Egypt thus far, yet suddenly there seems to be more and more of these rare numbers showing through the assembled data on circular “altars” upon closer inspection, which implies there is indeed significant overlap.

There are other patterns showing through the data – if I wanted a case in point that the number 1.0823232323 seems to have meant a lot to ancient American astronomer-architects, I probably needn’t look any further. We already know this number as “standard approximation Jupiter Orbital Period 4329.2929292 days / 10^n”, but there are apparently other reasons for it to have found favor in ancient astronomical formulas, and the same may be true for other numbers that have started to become familiar from examining ancient American calendar stones (“altars”).

Also, there have been discoveries that highlight the importance of closer examination of the planetary cycles themselves – quite notably, the discovery that the “Bat Palace Number” turns out to function as twice the ratio between Saturn Orbital Period and Saturn Synodic Period.

It comes to my attention that there may be more along such lines to be inferred from closer observation of the prograde and retrograde cycles of the planets.

While 1.0823232323 could be considered emblematic of Jupiter by way of being a simple fraction of its Orbital Period (divided by 10^n), given whole numbers for retrograde data (for which we will be “assured” that the simple minded ancients could only work with whole numbers) the ratio between Mars’ Synodic Period and Days in Retrograde calculates as 780 / 72 = 10.83333333.

What we are seeing may relate an often absurd amount of iconographic blurring or other related impacts on mythology brought about by changes in what is happening in terms of astronomy. In terms of the sort of mythographic studies I’ve pointed out like Brendan Crawford’s efforts to clarify the association of the planet Saturn with various ancient Egyptian mythological characters or “deities”

Even when there a very strong association might be made, there tend to be things that appear as if anomalies; as sensible as an association between Thoth and Saturn may be, there are ancient textual references that curiously involve references to the Sun, the Moon, or Mars.

To me, what we are seeing take place in the mythology may have meaningful parallels in what is taking place in the mathematics; there are ancient references to Saturn as “a better Sun” – an apparent Solar reference that may not make a great deal of sense outside of a connotation such as that Saturn’s Synodic Period divided by its raw Retrograde Period gives the inverse of the Solar Year. There’s something that’s decided “Solar” about something as “not Solar” as Saturn.

What we have just seen for Mars, 780 / 72 = 10.83333333 = Jupiter Orbital Period 4329.292929 / 4 / 100, may help to explain how Mars found its way into the discussion of Saturn, and etc.

I believe I have recently pointed out a number of facts about a certain set of numbers, including their exponential merits. We have a number of meter-like figures to consider, but when we go to ask which if any might have been afforded “primacy” on the basis of exponential merit, it seems to be 3.289868134 that comes out as one of the leaders, if not the leader.

In theory, while a meter based on the squared Radian would find usefulness in many equations because the squared Radian finds usefulness in many equations, the exponential use of such a “meter” would still be expected to have limitation. We don’t usually have that much expectation of getting exponential use out of the Radian itself. Sometimes we can find the Radian working as a data retrieval tool up to the 7th power or so, usually we’re probably doing good if we’re getting the Radian to work for us up to the 3rd or 4th power in general. A meter based on Radian^2 if itself squared then already equals Radian^4, so we probably shouldn’t expect a “squared Radian meter” to have exponential value past the second power of itself most of the time.

I could talk more about 3.289868134, including its origins in Munck’s work; 3.289868134 = Pi x (PI / 3) and 3.289868134 = 10.33542556 / Pi, but if anyone happens to be familiar with Carl Munck’s work, they may know that his equations and calculations told him that 10.33542556 was of major importance. I’m still quite impressed that his work managed to retrieve those facts even out from under the shadow of the Royal Cubit, which is so similar when presented as 6 Royal Cubits = 6 x 1.718873385 ft = 10.31324031 ft. To my knowledge, none of us have ever written the book about how to keep the two 100% sorted out, but they are obviously both of considerable importance.

I could also talk more about 1.315947254. It still appears in my notes abbreviated as “CHOL” because Munck’s extensive mathematical explorations seemed to have showed him that this number was important enough to make sense to us a his “geomathematical” coordinate for no less than the mighty Cholula pyramid. Even setting aside his potentially contentious “geomathematical” concepts, this number has great merit and very meaningful mathematical properties, and would have easily mattered to an ancient mathematicians who were aware of it.

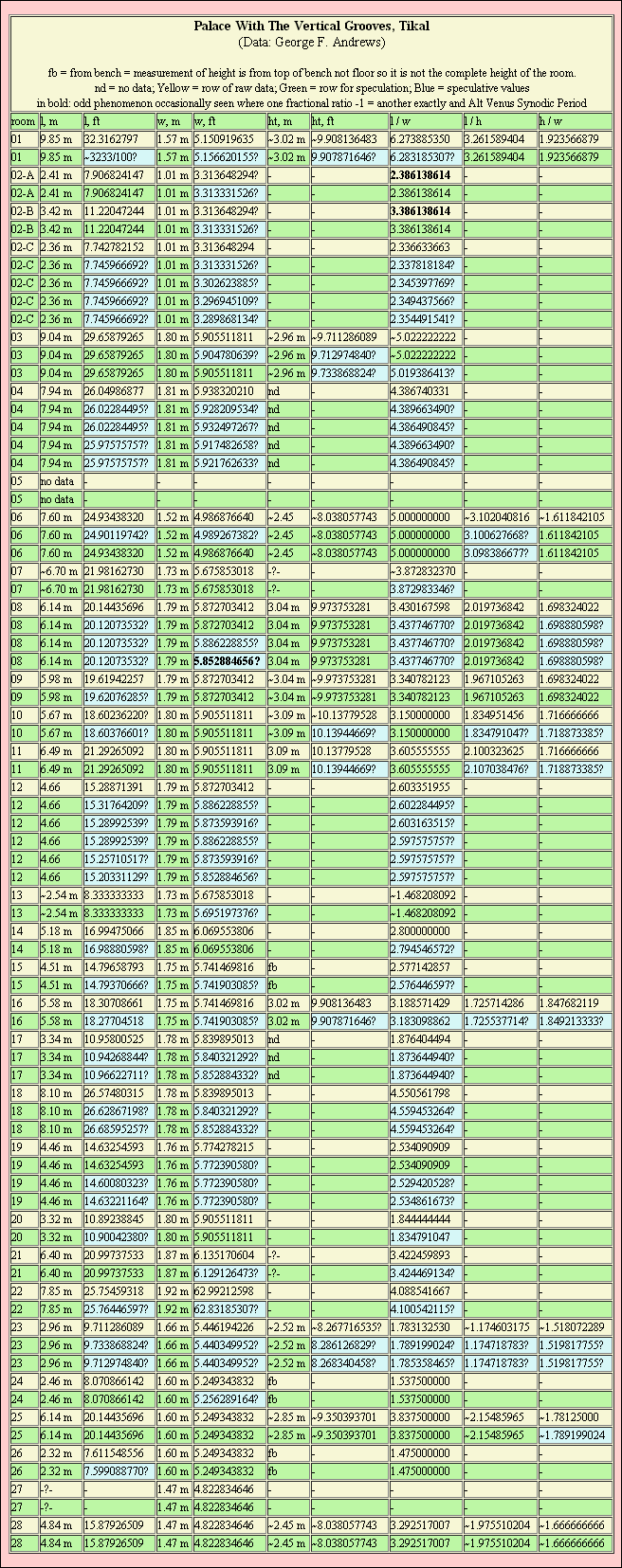
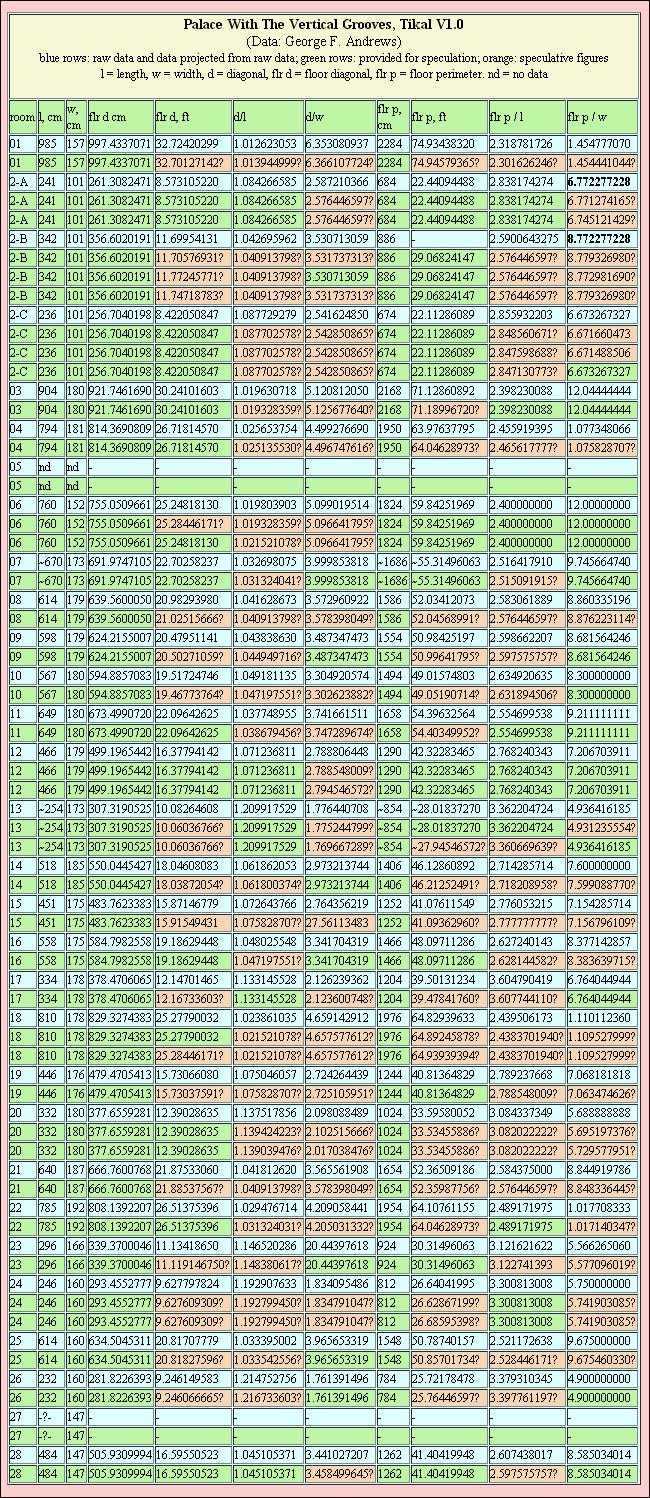
Some of my work with Andrews’ data suggests that we may have at least one example where an ancient architect may have thought enough of the number to display it both forward and backward in the same room by deliberately choosing a set of overall proportions that probably don’t make sense any other way and that may discourage us from trying to resolve the puzzle with a geodetic expression.

Simply put, 13.15947254 / 4 = 3.289868134, which has earned 3.289868134 a tentative nomination as a “Cholula Meter” before although I’m allowing the term to fall into disuse because I’m still not sure that we should try to think of 3.289868134 as a meter. As tempting as the idea of ancient American metric may be, or for as many as may have been tempted by the prospect, there are likely still considerable merits in any anti-metric arguments that address the possibility of common use of metric in archaeology being able to obscure important metrological or astronomical data.

At any rate, in case no one’s tried it at home yet, a consequence of some of the preceding facts is that

3.289868134^2 = 10.823232323

The subject of the set of number consisting of these and related figures sometimes falls by the wayside, but another consideration that keeps trying to move the discussion to the front burner, so to speak, is that the most solvent approximation of the Saros Cycle may not be the most accurate one.

Rather, the most useful and relevant approximation of the Saros Cycle of approx. 6585.3211 days may actually be 13159.47254 / 2 = 6579.736270, with the accuracy being comparable to that involving the Half Venus Cycle and its approximations, minimum accuracy being very roughly 1 in 1000 days.

3.289868134 aspires to re-enter the discussion which has lately begun to turn toward the recognition of Jupiter and Saturn cycles by the Maya, because using rounded numbers, Jupiter Synodic Period 399 days / Jupiter Days in Retrograde 121 = 3.297520661, something that would likely benefit from being approximated as 3.289868134.

An alternate of course might be to demarcate this as equal to 3 Indus Feet, which should not be overlooked (or go untested) but 3.289868134 may be most worthy of examination for being part of a general trend being observed here, particularly if an argument ends up resting on exponential value.

Surprisingly, even though I consider Indus Units as probably directly derivative of Megalithic Feet, I do not associate Indus Units with exponential value, let alone the sort of exponential feats that the putative Megalithic Foot value of 1.177245771 is often capable of. I have to do no more than simply square the standard Indus Foot value to come up with something I have no idea whatsoever what to do with. The likelihood is probably that ancient people preferred to think of it – and work with it – as the Megalithic Foot rather than the Indus Foot or its derivatives.

In talking about the early efforts with the calendar stones, I’ve mentioned that there seemed to be considerable relevance to be afforded to a figure of 30 / (Pi^2) = 3.039635509 in some of the calendar calculations.

Are we all that surprised to discover that 20 / 3.039635509 = 6.579736270 and 40 / 3.039635509 = 1.315947254?

For all this (and more) we should probably expect to see a good deal of 1.315947254 and related numbers appearing at various sites to help afford them with much greater functionality for astronomical calculations and data storage and retrieval.

However there may still be more to the story, speaking of exponential functions. It’s rare enough that we get valid figures as the square roots of important numbers; far more often these square roots are things that need to to be discarded because they don’t belong to the system in question, although there is still some question about what all the ancients would have done to compensate for that.

The standard figure for the Jupiter Orbital Period is made more attractive by having one of these relatively rare valid square roots, which is

sqrt 4329.292929 = 65.79736263 — it’s managed to drift a bit at the last several places from 20 / 3.039635509 = 6.579736270, as these figures often do when working to only 10 digits, but it’s quite obvious what it is.

Perhaps even more surprisingly, 65.79736263 also has a valid square root, which is

sqrt 65.79736263 = 8.111557349 = 16.22311470 / 2

Thus the ancient Mayans have managed to intrigue us with their references and calculations until we have learned yet another remarkable thing about the 1.622311470, which I insist that it seems is one of a small handful of essential numbers that the ancient architects seemed eager to try to incorporate into virtually everything, 1.177245771 being another such number.

Of course, we have also been seeing a remarkable amount of the Hashimi Cubit of 1.067438159 ft (see Egyptian Royal Foot, Sothic Cycle, Hipparchic Cycle) in the calendar stones, is what it looks like. Even though we have found it through completely unrelated functions, are we completely surprised to find that besides getting the Jupiter Orbital Period approximation from 8.111557349 = 16.22311470 / 2 at the fourth power, and a probable Saros Cycle approximation by squaring 8.111557349 = 16.22311470 / 2, that if we cube 8.111557349 = 16.22311470 / 2, we get 8.111557349^3 = 533.7190804 = 1067.438159 / 2.

I didn’t even know that 1067.438159 / 2 had a valid cube root, but apparently they did the way they have grouped these numbers together so enthusiastically, and as it increasingly appears, consistently.

Now, if you’ve been able to follow along with some of my posts this year, going back to the return to the legend of the Lake Moeris pyramids in Egypt, and the Faiyum Oasis region where they were reported and its architecture, you hopefully already know that a “Faiyum Number” was recognized as seemingly being recurrent in the ancient architecture of the Faiyum Oasis, and then eventually I returned to Tikal to try again to tackle the “Bat Palace”, only to find an apparent solution in the form of the “Bat Palace Number” which soon proved to be double the “Faiyum Number”.

I’ve been throwing out “maybe we shouldn’t be too surprised” left and right in this post, but let’s all go ahead and be however surprised as we like about this one, because that’s what I’m going to do.

So we have seen (1.622311470 / 2) giving off astronomical data at the second, third and fourth power, which is so remarkable that surely our luck has run out by now, right?

(16.22311470 / 2)^5 = 35.11730789

Hopefully everyone knows what that is – it’s twice the projected perimeter of the Great Pyramid’s missing apex section (divided by 10^n).

That was the next thing I was going to talk about, is how we usually don’t get far after finding a new Mayan Wonder Number before we being to recognize its presence in the Great Pyramid or at Stonehenge (what a remarkable thing that is in itself, and we are still generally using so few of the numbers present at either one, that’s almost all I ever talk about at Stonehenge is just the sarsen circle).

We did already know this was here because back when the Faiyum Number was recognized, we did find out that it traced all the way back to Egypt’s 4th Dynasty at least because of its presence in the model of the Great Pyramid; I guess it’s just the drama of the presentation now that we know what the Bat Palace may be trying to say

Perimeter Great Pyramid Missing Apex Section 175.5865396 ft

(351.1730789 x 10) / 2 = 175.5865396)

So (16.22311470 / 2)^5 = 35.11730789 gives us not only another very clever way that 16.2231147 was incorporated into the Great Pyramid, but all the astronomical data that comes with 16.22311470 / 2, but in observing what may be “vicarious” occurrence of the same number between ancient Egyptians and ancient Americans,

1 / 175.5865396 = 5.695197379 / 10^n.

The reciprocal of the perimeter of the Great Pyramid’s missing section is the Tikal “Bat Palace” Number.

So, (16.22311470 / 2)^5 = (2 / Bat Palace Number) x 10^n

At (16.22311470 / 2)^6 = 2.848560569 x 10^n

Now has our luck run out? Well, no, because 2.848560569 / 2 = 1.424280285, which is one of the original Tikal “Wonder Numbers” = 1.676727943 / 1.177245771, which was later found at Stonehenge and at Giza — but that’s got to already be much more than we can rightfully expect from exponential function here, obviously.

Yet there is still another round.

At (16.22311470 / 2)^7 = 2.310822428 x 10^n, we are still on a familiar track an in the realm of what is useful. 2.310822428 = AEMY Megalithic Yard 2.720174976 / Megalithic Foot 1.177245771, which is all we need to do generate simple fractions of the “Best Eclipse Year” value.

At (16.22311470 / 2)^8 = 1.874277728 x 10^n, we no longer seem to have functional fractions of the Venus Orbital Period (i.e., 224.8373808 / 12 = 1.873644840 and etc), and yet we still haven’t run out relevance.

2 / 1.874277728 = 1.067077718, which is 1/1000th of the Great Pyramid’s projected base diagonal length at the proposed pavement level (i.e., the proposed diagonal for Munck’s own model of the Great Pyramid)

We can actually go at least as high as (16.22311470 / 2)^9 without running out of things we can recognize, although we may be truly pushing the limits of usefulness now – we are about at the point now where Stonehenge’s reach may begin to exceed its grasp, and perhaps several particularly attentive readers will be able to think of exact what I mean by that.

If it helps to have a reminder, the Hashimi Cubit is almost the cube root of the Remen – almost. Standard Remen = 1.216733603 ft, Hashimi Cubit cubed = 1.067438159^3 = 1.216264895. What do we do about that, and what did the ancients do about it exactly?

We have certainly learned about new data we can extract from the base of the Great Pyramid by using the numbers we can find at the top. Do the Great Pyramid’s sometimes somewhat odd proportions make more sense now? They do to me!

We have also learned that for as much accumulated incentive as there may already be for the ancients trying to include 1.622311470 into all of their permanent architecture, there was still more to the story, just as there is probably still more to the story even now, just as there is still more to the story of the related astronomical calculations.

As I begin to look more closely at “altars” from Tikal and elsewhere including the “Altar de Sacrificios” site in Guatemala, for several of the altars from this site, using data from both Maler and Morley, I don’t know if it’s the right answer, but I should note that for Altar 1, the total diameter of the glyph band should be (82 + 25 + 25 = 132 cm) = 4.330708661 ft = 346.4566929 / 8 / 10^n = ~346.62 / 8 / 10^n and for Altar 3 the diameter inside the glyph band should be 108 cm = 3.543307087 ft, so there we have what look like the Eclipse Year and Lunar Year both associated with the glyph band diameters of these artifacts.

 

One of the altars in question at Altar de Sacrificios in Guatemala, as photographed by Teobert Maler, showing the band of glyphs on the top surrounding a smooth center.

 

A little bit more that has been observed in pouring over the data for the “altars”:

Interestingly, when we bring Lunar Year into conjunction with Saturn’s primary values, the Orbital and Synodic Periods

Synodic Period 378 / 354 = ~1.067438159
Orbital Period 10759 / 354 = ~30 / (Pi^2)

These equations work precisely with established values.

So when we are seeing 1.067438159 or 30 / (Pi^2) in these altars, one of “x” number of things they represent are links between the Lunar Year and Saturn’s Cycles, meaning they are things one would use to expand a statement of Lunar Year data into a statement of Saturn data as well.

We being to see some of what looks like (24 Remens x Pi) / 10^n = 9.173955233 = 1 / 1.090042380

Why would we see this? In context,

Saturn Synodic Period 377.8016633 / 9.173955233 = 411.8198244 thus far the preferred form of the Full Moon Cycle of “411.78443029” days, and

Saturn Synodic Period 377.8016633 x 9.173955233 = 346.5935546 thus far the preferred form of the Eclipse Year of ~346.62 days

It does not appear to be so conversant with Saturn’s Orbital Period (?) but thus 9.173955233 distinguishes itself as a particularly important link between key Lunar Values and the Saturn Synodic Period.

–Luke Piwalker

 

 

 

 

 

A Glossary of Sorts…

I was watching a video a little earlier that explores some of the characteristics of science vs characteristics of pseudoscience. That’s kind of a tender spot for me, because it’s quite often that work I cite gets that stereotypical label lobbed at it, including Thom’s and Munck’s. I can say I think my own work technically cleared the criteria for not being pseudoscience with generally good marks, although there’s one characteristic of pseudoscience that’s tricky, concerning specialized or evasive jargon, where it might be easier for the casual observer to get the wrong idea.

It must seem from reading some of these posts that I have an endless collection of strangely (and often unimaginatively) named mathematical constants and a bottomless hat full of metrological units with which to disorient my audience and achieve my conjuring tricks, but that isn’t really how it works at all, and hopefully an overview like this can help clarify that.

Here are most of the numbers that currently have nicknames, and I’ve already padded out the list with several key astronomical values that don’t necessarily belong filed there. The main metrological units I work with are also represented even in this limited table, which I like to think is far less specialized knowledge than exists in many branches of science. It is absolutely astonishing what can be accomplished even with the humble collection of numbers seen here.

I think that’s most of them, I can’t be missing too many?

Anyway, I thought something like this might be in order for readers’ reference since I am sometimes lapsing into referring to these numbers by their “nicknames” for convenience rather than to their numerical values.

These would also make an interesting starting palette of numbers for anyone wanting to begin experimenting with the remarkable relationships between many of these numbers, but for the sake of that I should have included the proposed Sacred Cubit of 2.091411007 ft among the metrological units.

Observant readers may catch a glimpse of why I work with such a restricted spectrum of Royal Cubits – I sanction 1.720116607 ft as a value for the Royal Cubit because I’m forced to by geometry because I try to honor the geometric relationships between units (as much as humanly possible) that involve squares or rectangles, and this sort of geometry gives a Remen of 1.216733603 a Royal Cubit of about 1.216733603 x sqrt 2 =  1.720721163 ft, while the standard Royal Cubit of 1.7188733385 is more realistically related by diagonals to the short Remen.

Mathematics, geometry, accuracy, and the observance of square/rectangular relationships between units demand this, yet because 1.720116607 is a value in Megalithic Feet, that’s what it registers as rightfully being is Megalithic Feet and NOT a Royal Cubit. In the same way, most if not all of the potential alternate values for the Royal Cubit may end up claimed by other metrological units as their own, which will mean they are something other than Royal Cubits. We’ve learned some of that along the way although there is still more to explore.

Anyway, an important point here is that not just me trying to keep the number of Royal Cubits down to a minimum, it’s the very system itself, and hopefully the another point is that this is probably really nowhere as difficult as its been trying to look.

Looking back on years of experience, the most difficult thing has often been just trying to take it seriously, but a great number of shaky observations have been lavishly explained in the fullness of time. The right number often arrives well before any definitive understanding of why it is the right number – we are even now learning more of the secrets of the Aztec Sun Stone and why it literally must be an astronomical dictionary and calculator.

The work I’m attempting at the moment is particularly exciting even though its time consuming and often unrewarding. It means fewer site studies and fewer blog posts for the moment, but it’s something any of us might dream of to be able to check the mathematics of the celestial objects that even orthodox archaeologists or astronomers can agree are being referenced by the architecture or artifacts, against the mathematical and metrological values in the objects themselves.

As far back as my collaborations with Michael Morton we though both should show us the same thing, but this is still so much a matter of pulling ones self up by their own bootstraps sometimes that we still may not have the best tools to explore this. Recent work has nonetheless been tremendously encouraging in this respect.

Regarding clearing the air about pseudoscience, there’s already a lot of material out there attempting the subject of pseudoscience that merits correction, starting with sources that have tried to stick this label to Thom. I have a meager paper on Academia.edu that even such as it is, I hope does an adequate job demonstrating how several sources often credited with successfully dismissing Thom and his Megalithic Yard actually tendered data that supported his arguments.

Perhaps one of the worst perils waiting for all us to fall into when attempting to sort science from pseudoscience, is that fact that in a number of cases, scientific protocols may be inadequate or lacking altogether to address what the alleged pseudoscience is contenting.

The worst case scenario would be that the scientific community may have no scientific protocols whatsoever for evaluation of certain alternative theories. Nobody in science is likely to draw up protocols for what stone-age rocket scientists should look like if they already don’t believe in them, correct? Why would anyone draw up protocols for evaluating something they don’t even believe in?

While I think persons on either side of the fence, orthodox or alt, should be entitled to set up a model and see what it takes to knock it down, that business of having made up your mind in advance about a matter may well be one of the most important distinctions of what makes up a pseudoscience. Go figure.

For now, someone probably still has some explaining to do as to why the Coyolxauhqui Stone seems to get itself described as having such a lunar character to it, unless some attributes of Venus in the mix are perhaps being overlooked.

–Luke Piwalker

The Sun Stone and the Eclipse Year

I have written before about the mathematical calendar formulas that may have been written into the Aztec Sun Stone. It has come into focus again because one of its key numbers may appear in the original measures of the Stonehenge ditch according to some of the data available, shortly after also appearing in the design of Hadrian’s Library complex. Now, it is also subject to focus because as we begin to look at the work of Susan Milbrath, we find references therein to a possible symbolic association between the Sun Stone and the Eclipse Year.

I might have stumbled over it before and forgotten but I can’t find reference to “Eclipse” or “346” in the first comprehensive post I tried to write on the subject. Whether or not I agree with Milbrath’s perspective on the question, there do indeed seem to be some interesting connections between the proportions proposed for the calendar stone and the Eclipse Year figure I call the “Best Eclipse Year Value” of 346.5939351 days.

Here is an interesting series that works all the way to the 5th power of the radius of the Sun Stone that at very least connects the Bat Palace Number (the internal ratio of Saturn’s cycles) to the Best Eclipse Year at the 4th power, if the inclusion of the Great Pyramid in the equation seems too out of place to anyone.

(Great Pyramid diagonal at proposed pavement level: 1067.077716 ft, adapted from raw data of (3018.110298 / 4) x (sqrt 2) = 1067.063129)

(1067.077716 x 2) / ((Sun Stone Diameter 3.747289674)^1) = 5.695197376 / 10^n = Bat Palace Number
(1067.077716 x 2) / ((Sun Stone Diameter 3.747289674)^2) = 151.9817754 = (30 / (Pi^2)) / 2; (30 / (Pi^2)) is part of prior calendar stone proceedings
(1067.077716 x 2) / ((Sun Stone Diameter 3.747289674)^3) = 40.55778673 = 162.2311470 / 4
(1067.077716 x 2) / ((Sun Stone Diameter 3.747289674)^4) = 10.82323232
(1067.077716 x 2) / ((Sun Stone Diameter 3.747289674)^5) = 2.888282803

The same digit three times starting at the second place like 2.888282803 is usually an indicator of seeing a simple fraction or multiple of the Best Eclipse Year.

Case in point, 2.888282803 x 120 = 346.5939364 Best Eclipse Year = ~346.62 days

I found this series quite interesting for a number of reasons in addition to those already mentioned. 10.82323232 is 1/4 of Jupiter Orbital Period / 4 (I noticed early on in Mayan studies that they seemed rather fond of 10.82323232 for some reason), but perhaps what is most interesting here is that in terms of diameter, the Aztec Sun Stone has a Mayan Twin at Yaxchilan according to the data.

I find it quite remarkable that the thickness given for the Yaxchilan altar by Morley (via Carolyn Tate) is .33 m = 1.082677165 ft, and I’m going to take a wild guess the intended figure was 10.82323232 / 10 ft.

It’s as if 3.747289674 really is a calendar number for all seasons and they knew that well.

(Meanwhile, in the next consecutively numbered structure at Yaxchilan after the one with the Sun Stone’s twin, there is described by Morley via Tate an altar with an already suggested diameter / thickness ratio of D/T R = 4.055778682).

There’s an odd little bonus that comes out of this, which is that 3.747289674 / 1.082323232 = 3.462264841. We’ve probably not much to do with that per se because we have numerous better things for approximations of the Eclipse Year, but somewhere out there someone might be suggesting that (sqrt 12) = 3.464101615 could be a suitable approximation of the Eclipse Year / 100.

My preference of Eclipse Year values is still “Best Eclipse Year” of 346.5939351 days, I really don’t pay much attention to the other ones unless they manage to impose themselves on something where 346.5939351 doesn’t fit but they haven’t had much luck with that so far. An even better approximation of the Eclipse Year can be had with valid numbers but it’s out of synch with the system a bit and lacks the resonance it needs to volunteer more often, so 346.5939351 frequently seems free to dominate.

I’d like to point out though that although the textbook figure for the Eclipse Year is 346.62 days, the semi-canonical translation of 1/19th of a Saros Cycle should be likely be 6585.3211 / 19 = 3.465958474. (6585 / 19 = 3.465789474). In other words, the figure I use is (once again) closer to the figure that may actually arise from traditional formulas.

At any rate, if you caught the (sqrt 12) trick, you probably thought of trying 12 / 3.462264841 = 346.5939364 / 100. In other words, 3.462264841 IS 346.5939364, it’s just written backwards.

I should point out that the diameter of the Sun Stone does enjoy good interactivity with the Best Eclipse Year value. For the Sun Stone, Radian / Pi is the double short Solar Year, and the speculative model of the Sun Stone allows for both long and short Solar Year, so that Radian / Pi probably can be considered a specifically indicated number.

(Radian / Pi) / ((Sun Stone Diameter 3.747289674)^1) = 4.866934409 = 1/10th inner sarsen circle radius Stonehenge
(Radian / Pi) / ((Sun Stone Diameter 3.747289674)^2) = 1.298787879 = 1/80th outer sarsen circle diameter Stonehenge
(Radian / Pi) / ((Sun Stone Diameter 3.747289674)^3) = (Best Eclipse Year 346.5939366) / 10^n
(Radian / Pi) x ((Sun Stone Diameter 3.747289674)^1) = 2 / Real Mayan Annoyance

Also for the Sun Stone, circumference / Best Eclipse Year = 6793.227761 / 2 / 10^n, where 6793.227761 is trying valiantly to earn its stripes as a legitimate version of the Nodal Cycle.

11.77245771 / 346.5939366 = 6793.227732 / 2 / 10^n

Combined with the A form of the Calendar Round, 11.77245771 / Pi = 3.747289674 may perform another vital function linking the Calendar Round to the fourth root of the Saros (if the Saros generated can be verified as legitimate)

Calendar Round A 18983.99126 days / 3.747289674 = 5.066059181 x 10^n; 5.066059181^4 = 6586.899474 / 10; Saros Cycle textbook value 6585.3211 days

We also get another Saros figure by multiplying Calendar Round 18983.99126 x Best Eclipse Year 346.5939366 = 6579.736262, which may have more substantiation than the figure generated from a 4th root; 6579.736262 seems to be part of a premiere pair of approximations characterized by having the 1.000723277 relationship; 6579.736262 x 1.000723277 = 6584.495234, what might be called the “Best Value” for the Saros, although the greater resonance and solvency probably belongs to 6579.736262.

I think sooner or later it’s going to come up that a reason that some of the preferred approximations for longer Lunar cycles like these may still be unsolved is because there may be multiple representative sets – suppose the Saros, Nodal, Metonic or other Lunar cycles were such an important business that they granted them two table rows and six different variations instead of one row and three variations, that might explain quite a lot but I”ll believe it when I see it.

Certainly with the variances exemplified by actual Mayan Codices or implied by obvious operations (Mayan Calendar Number 819 / Venus Orbital Period 225 = 364 / 10^n not 365 / 10^n), the Solar Year along with the Synodic Periods of Venus and Mercury have been afforded multiplicity.

It’s also interesting to wonder if the same may apply to the Lunar Month / Lunar Year, and whether this might at last allow the Squared Royal Cubit to be a legitimate Lunar Month. So far it has been excluded by the very systematics involved themselves, but a separate situation might be permissive.

In some of the work I’ve done lately there’s been emphasis on the difference between the Eclipse Year and a simple fraction of the Metonic Cycle. In canonical numbers one might be able to get away with “Jupiter Orbital Period x 8) / 10^n = Eclipse Year and Eclipse Year x 2 x 10 = Metonic Cycle” but something a little more intricate and versatile seems to happen with the numbers I use, where again, we seem to be able to actually distinguish between the Eclipse Year and the most outstanding candidate so far for the main value of the Metonic Cycle.

The main thing that got me looking at Morley’s work again is because I have a number of quotes of altar proportions from a multivolume source not indicated in my notes (my first guess is the multivolume Inscriptions of the Peten). In Volume 3 of the mysterious source work, there is an altar associated with a Stelae 27 (likely a sizeable site?) given dimensions of Diameter .56 m = 1.837270341 ft, Thickness .71 = 2.329396325 ft.

.56 / .71 = .7887323944 = 1 / 1.267857143.

I’m far from sure I have any idea what these numbers mean yet, but there is at least one valid number that resembles it. 1.264223085 is one of them.

A curious thing about this is that from the raw data 1.83270341 x 2.329396325 = 1 / 2.342418159 but the resemblance to its own reciprocal becomes more pronounced when I begin to try to “fine tune” the values. Probably alternately, 2.342418159 / 2 = 1.17120906 = ~117 / 100 so the long “Dresden” versions of Mercury (117) and Venus (585) may be riding along there?

I’m starting to think that 1.837270341 may mean 1.838737943 for the diameter, with the resulting circumference being diameter 1.838737943 x Pi = circumference 5.776565613.

What that would probably do is land the number near a busy intersection of equations; also there seem to be other altars that share some of these proportions (see Chinkultic and Tzimin Kax?)

1.838737943 is probably a new Wonder Number. I’ve been seeing this number and began to realize it was probably something important, but I hadn’t quite guessed much more. One thing this number is, is the long “585” day version of the Venus Synodic Period, times Pi.

5.776565613 / 4 = 2.888282807

A little while back in this same post, we saw

“(1067.077716 x 2) / ((Sun Stone Diameter 3.747289674)^5) = 2.888282803

The same digit three times starting at the second place like 2.888282803 is usually an indicator of seeing a simple fraction or multiple of the Best Eclipse Year.

Case in point, 2.888282803 x 120 = 346.5939364 Best Eclipse Year = ~346.62 days”

Hence, 5.776565613 = 346.5939368 / 60

Possibly what they did with the a x b = ~1 / b factor is set it up to juggle both versions of the Venus Synodic Period, although this remains to be seen.

Interestingly, Morley seems to describe another altar associated with the same stela (Stella 27) at the same unspecified site with a diameter of .33 m = 1.082677165 = ~1.082323232. The thickness is the same (.71 m).

.71 / .33 = 2.151515152 / 10

.33 / .71 = 4.647887324 / 10

These rather resemble the sqrt of 2160 and its reciprocal: sqrt 2160 = 4.647580015 x 10 and (1 / 4.647580015) x 10 = 2.151657415, which in reverse gives one of the already suspected figures for the meaning of “.71 m”:

1.082323232 x 2.151657415 = 2.328788808. I believe the possibility of this number has been reported in the vicinity of Tikal before (nominated as probable width of stairway of Topoxte Structure C, data from Pinto & Noriega 1995).

In the same vein, in pouring over my data tables for circular altars it came to my attention that there was no data present for the “Coyolxauhqui stone“, one of the more famous Aztec altars.

In looking to amend this, I stumbled over a blog post by Steve Minor that purports that a museum label from the Templo Mayor Museum that states “…its circumference is irregular, with a maximum diameter of 3.25 m (10’8″) and a minimum of 3.04 (10′); its thickness is 30 centimeters (about 1′) and it weighs about 8 tons.”

I’m suprised this hasn’t been mentioned before because the value 3.25 was already in my tables where it had been recognized as 10 “Hashimi Cubits” = 10.67438159 ft, but perhaps I was cautious because of the lack of data. I suspect that what happened is that I might have obtained only the diameter value of 325 from a paper by Emily Umberger?

The dataset quoted above gives as basic parameters

Major diameter 3.25 m = 10.66272966 ft
Minor diameter 3.04 m = 9.973753281 ft
Thickness 30 cm = .3 m = .9842519685 ft
Major / minor diameter ratio 3.25 / 3.04 = 1.069078947
Major diameter / thickness 3.25 / .3 = 10.83333333
Minor diameter / thickness 3.04 / .3 = 10.13333333

The last of these figures of course resembles the Greek Foot value, and the one just before it of 10.83333333 much resembles the suggested figure of 10.823232323 that seems to be recurring through these artifacts, which is after all a simple fraction of the standard primary Jupiter Orbital Period approximation of 4329.2929292 days for 4332.59, which I believe is good accuracy especially for such a large figure.

These “altars” thus may have a possible common theme of Jupiter running through them.

It eludes me at the moment whether the Greek Foot is to be expected to have astronomical significance besides being a simple Solar Year fraction (365/360 = 1.0138888888), but given its relationship to the Remen it’s probably fair to credit it with more.

I suspect that 3.25 / 3.04 might be intended to represent 1.069734371. It may often keep a low profile so it doesn’t collide with 1.067438159, but it is a Wonder Number in its own right and it belongs to one of the original Wonder Number series located at Tikal.

We start by dividing the orbital period of Venus in half, then dividing it by (Pi / 3)

(VOP 224.8373808 / 2 = 112.4186904) / ((Pi / 3)^2) = Wonder Number 1.0251355300 x 10^n

(VOP 224.8373808 / 2 = 112.4186904) / ((Pi / 3)^3) = (1 / Wonder Number 1.021521078) x 10^n

(VOP 224.8373808 / 2 = 112.4186904) / ((Pi / 3)^4) = (1 / Wonder Number 1.069734371) x 10^n

All this and more makes 1.069734371 a valuable piece of data because of the data we can easily extract from it, and the resultant series may well be THE most profound series ever discovered, because it also contains 1.177245771 and BOTH of the two most powerful mathematical probes ever discovered, 2 / 1.622311470 and 10 x (1 / (sqrt 60)).

If we accept 10.67438159 as the diameter and 1.069734371 as the Major/Minor diameter ratio, the minor diameter becomes 10.67438159 / 1.069734371 = 9.978534746

I’m not certain what to think of that; it may be something of an exotic number and possibly an awkward one, but it does happen to be a simple fraction of one of the figures currently used for Jupiter’s Synodic Period

9.978534746 x 400 = 399.141390 the “A Value” of Jupiter Synodic Period (“textbook” value 398.88 days; “B value” is thought to be 399.4300799).

Because the artifact is an ellipse rather than a regular circle, even though it is not exactly a regular ellipse in shape either, we may be able to more closely approach what may be its original symmetrical design by entering the major and minor diameter into calculations for the perimeter of an ellipse

The linear eccentricity may get away with being something like perhaps 16 Megalithic Feet (?) = 16 x 1.177245771 = 1.883593234 x 10^n.

It may be almost unavoidable unless these calculations are upset by adjustments to the major or minor diameter, that the perimeter is going to turn out to be 16.22311470 x 2 = 32.44622940, which may have a great deal of reason for being present if this can be demonstrated by further explorations.

Tentatively – and we may want to take another quick look at the equations above that involve the Great Pyramid’s projected 1067.077716 base diagonal at the proposed pavement level and its exponential interactions with the diameter of the Aztec Sun Stone, before we observe

32.44622940 / 10.67438159 = 3.039635517, there’s 30 / (Pi^2) again, that we’ve seen repeatedly in the proceedings of even very few calendar stones

32.44622940 / (10.67438159^2) = 2.847598703, the Double Faiyum Number = the Bat Palace Number / 2.

32.44622940 / (10.67438159^3) = Great Pyramid diagonal at pavement level / 4 / 10^n

The two can be multiplied at least one power as well, so here we see 1.067438159 not only functioning up to the FOURTH power, but interactive with the Great Pyramid diagonal in the process.

I find all four of those equations rather encouraging.

Before I forget, there is something important I should point out lest someone overlook it, which is quite easy to do when there is so much to consider, but the suggested diameter of 10.67438159 is intimately related to the value 11.77245771 / Pi that seems to recur through a number of cited calendar stones (“altars”), including the Sun Stone and it’s partial “twin” from Yaxchilan

11.77245771 / Pi = 3.747289670 = 4 / 1.067438159

As a length measurement, 3.747289670 ft would be a value in Hashimi Cubits / Egyptian Royal Feet, but one important reason of many that this value was probably settled upon for the diameter of the Aztec Sun Stone is because 37.47289670 is a simple fraction — 1/6th — of the Venus Orbital Period of 224.8373808. 224.8373808 / 6 = 37.47289670.

We have more to learn about the Coyolxauhqui Stone, but suffice it for now that it might well be equipped to be on the very same wavelength as other major calendar stones.

–Luke Piwalker

 

 

Planets in Captivity? Of Jupiter and Saturn

Kind of a strange story, but having been smitten with the idea that a particular number ((10 Megalithic Feet / Pi) x 10^n = 3.747289674) might have appeared in the original measures of the Stonehenge ditch because it also seems to appear in some of both Aztec and Mayan calendar stones like the Sun Stone (and in the recent analysis of Hadrian’s Palace at the ends of the cistern), this managed to pique my curiosity about the subject again and got me looking at what data I have on ancient American altars.

I went to have another try at one of the numerous unsolved Mayan altars and ended up looking at things that notably seemed to have do with Jupiter and Saturn.


Altar at Altar de Sacrificios site, photographed by Teobert Maler. This would have to be the altar described by Maler’s texts for which in centimeters we are given Diameter 160 cm, Thickness 70 cm and “Atop pyramid of main temple… concentric band of glyphs 25 cm wide, surrounds a smooth circular surface 82 cm in diam. The band of glyphs has a smooth outer edge 14 cm in width.”

82 + (25 x 2) + (14 x 2) does indeed equal 160 cm, so at least we know that things add up correctly in his description. Maler’s measures convert to:

160 cm = 5.249343832 ft
70 cm = 2.296587927 ft
82 cm = 2.690288714 ft
25 cm = 0.820209973 ft
14 cm = 0.459317585 ft

Thickness 70 cm = 2.296587927 ft x Circumference (5.249343832 x Pi) = 378.7372052 / 10^n; Saturn’s Synodic Period about 378 days (378.09)

Radius 5.249343832 x Circumference (5.249343832 x Pi) = 86.569850404 = 43.28425202; Jupiter’s Orbital Period = about 4332.59 days

I found this especially interesting because recently I proposed a certain value for a conspicuously recurring measurement inside the Bat Palace (Palace of the Windows) at Tikal, only to discover it is almost identical to twice the ratio between the Orbital and Synodic Periods of Saturn.

Jupiter Orbital Period 10759.22 / Jupiter Synodic Period 378.09 = 2.845676955; Faiyum Number x 2 = Bat Palace Number / 2 = 2.847598688.

When I went to see if I could expand my collection of ancient American altar data with Google searchesto perhaps learn more about these matters, I found a paper by Susan Milbrath talking about how the end of the Katun in conjunction with the dual retrograde of Jupiter and Saturn seemed to be the motivation for the creation of new altars at Tikal.

The Maya Katun Cycle and the Retrograde Periods of Jupiter and Saturn
Susan Milbrath

“The incidence of the actual records of Katun on monuments of the Classic and Postclassic periods seems to be significant when we look at the patterning in relation to retrograde. At times that Jupiter or Saturn were in retrograde at Katun end, the Tikal monuments most often record Katun endings. Tikal showed a preference for recording Katun dates at times that Jupiter or Saturn was in retrograde motion. Conversely, during the periods (hiatus and Terminal Classic to early Postclassic) when there is no correspondence between the Katun ending and the retrograde periods, these Katun records are lacking, especially at Tikal, where the Katun cycle seems to have strongest and longest development. In the Postclassic, Mayapán seems to revive the tradition of recording Katun endings during the epoch when the planetary retrograde coincided with the Katun end.

The celestial dance performed by Jupiter and Saturn in retrograde motion at Katun end marked time at important periods in Maya history. There is a clear pattern linking recorded Katun endings to dates when either Jupiter or Saturn was in retrograde motion, especially at Tikal, a site that was the largest and longest occupied of the Classic Maya cities. The first epoch of such a correspondence was in the Early Classic period. The written record ceased on Tikal monuments around the time the planets failed to perform their retrograde dance at Katun end. It is noteworthy that at Tikal, where interest in marking Katun endings seems to be exceptionally well developed, the hiatus in monumental records lasted until the Katun ending in 692, when there was a renewed correlation between the Katun ending and the timing of retrograde events. Furthermore, Tikal shows a great focus on Katun endings by erecting special twin–pyramid complexes to house Katun ending monuments beginning in 692. The last inscription at Tikal was the Katun ending in 869 (10.2.0.0.0; Stela 11), which coincides with a spectacular conjunction of the two planets located very close together at their second stationary points, when they were especially bright in the sky. After 889, throughout the central Maya area there was an abrupt halt in the long sequence of monuments marking the Katun end precisely at the moment that the synchronicity of the planetary retrograde with the Katun ending came to an end.”

If she’s right, it may be very matter of fact, yet it somehow it seems remarkably revolutionary in that she would be providing an overarching rationale for the creation of new date markers that may not only take precedence over any other motivations, but may be able to function independently of any other motivations. 

In other words, astronomy and the way it was responded to at Tikal is probably going to mean that these commemorative markers are going to be made according to a planetary schedule regardless of what is going on in the community, and that the long hiatus in and decline of making new markers at Tikal may have corresponded to that was going on in the skies and not what was going on in the community or the environment. 

I think it raises questions about how any coinciding events recorded on date makers happened to come along on these dates, and even whether the worldly events referred to were genuine and whether they even needed to be.

However, something that caught my attention is the way that related themes like bondage and captivity (there are depictions of bound prisoners on some of the altars in question) could serve as euphemisms for the behavior of the planets in question – could a second planet joining a first in going retrograde be considered as being bound by, held captive by, or being taken prisoner by the first planet?



Tikal Altar 8 from Linda Schele collection (FAMSI)
Site: Tikal – Schele Number: 2005 –  Description: Altar 8, ca. ad 750-760. shows captive bound within a ball. – Architectural Feature: “altar”

In order words, just when we think the altar decorations have wandered off the planetary themes, maybe they haven’t after all and we just don’t quite understand the euphemisms in use. Again, as Milbrath would seem to have it, it’s these planetary “dances” that are the very reason for the altars being.



Altar 14 at Tikal, cited by Susan Milbrath’s article. This “Ajaw altar” at Tikal in Guatemala is similar to several at Caracol in Belize (FAMSI), which are noted to also have been commissioned to mark the completion of a Katun or Tun cycle.

I recently bought a copy of Vincent Malmstrom’s book “Cycles of the Sun, Mysteries of the Moon” – he at least seems to have a somewhat creative and halfway open mind (I’ve enjoyed a number of his webpages and some of his work on Mexican pyramids even loosely resembled some of the things I’ve worked with). In the index I stumbled over the phrase, “The Binding of the Years” which might also be in general accord with what I’m thinking about depictions of “the binding of captives”.

I think the attribution is limited therein to the Toltecs, but certainly it may have broader relevance including that while I know a diffusionist view of culture and mythology still isn’t the most popular even when everyone has a “Noah” in their folkore and all that, some of it might be traced back to equivalents elsewhere. I was very quickly reminded of Ixion from Greek Mythology, and of Mithra not only encircled by the circle of the Zodiac, but how perhaps the besting of the bull might be an equivalent to the conquering and binding of neighboring tribe members alleged as being shown by the Mayan altar scenes.

Wikipedia
Ixion was expelled from Olympus and blasted with a thunderbolt. Zeus ordered Hermes to bind Ixion to a winged fiery wheel that was always spinning. Therefore, Ixion was bound to a burning solar wheel for all eternity, at first spinning across the heavens, but in later myth transferred to Tartarus. Only when Orpheus played his lyre during his trip to the Underworld to rescue Eurydice did it stop for a while.


I’m also reminded a bit of material that Shawn Hamilton posted discussing Tikal. I’d suspected that the worst case scenario might be that components may have been conflated with references to lightning, rain, or thunder deities turning into references to persons at Tikal flinging lightning bolts at each other, and here it may turn out that perhaps such deity figures may not only be prominent in the mythology of the site, but even in the timing of creating new monuments.

Here’s a question – could Hesphaestos represent Mars at standstill or during retrograde? One could probably refer to a planet at standstill as “lamed”, if it isn’t going anywhere? I did pull some Mars numbers out of the inner sanctum of a Hesphaestos temple awhile back. Who might be an Egyptian equivalent?

Anyway, I will offer all this up in case it inspires or leads to anything productive or interesting for anyone. Ideally one can take it back to Egypt and use it in the search for clues. (I’m curious of the Egyptians were doing anything like this also but I’m generally distrustful of astronomy software, I’ve been following the “OCT” almost since it was announced and no doubt seen my share of “Your numbers are useless you because you used SkyThingie instead of SkyGizmo, SkyThingie turns stupid when you go back that far in time” discussions).

Everyone remember the lesson that my “Bat Palace Number” is built as 12 / Palestinian Cubit in feet, where the Palestinian Cubit takes legitimacy from essentially being the diagonal between what are probably the two most notable ancient Egyptian measures, the Remen and Royal Cubit (in “modern” feet also)?

Another thing we can make out of these two units, the Remen and Royal Cubit is the putative Sacred Cubit by multiplying their two values in “modern” feet, and I’ve very recently written about and posted diagrams of the remarkable mathematical properties of the resultant Sacred Cubit value

Remen 1.216733693 ft x Royal Cubit 1.718873385 = Sacred Cubit 2.091411162 ft.

Even now, new truths about the value of these two ancient Egyptian Units of paramount importance continue to come to light and it becomes easier and easier to see why they would have chosen the particular values for these units that they seem to have.

Note that what we see in the diagram, the profound power of the ratio 2 Pi to connect or transform these ancient units of measure, may have been one of the reasons for the Great Pyramid’s 2 Pi perimeter / height ratio. For me there is little doubt that the ancient Egyptians intended one primary function of the Great Pyramid’s proportions to be serving as a metrological reference, making it all that much more appropriate to proportion it in honor of the great metrological unifier 2 Pi.

We know that even if the Great Pyramid doesn’t honor the Remen and the Royal Cubit by actually using them in its physical proportions, they won’t be far behind by means of ratio. It’s been a long time since I first learned for example that Munck’s height for the Great Pyramid (from the pavement level) / 2 Pi / 2 Pi = the value of the Remen in feet x 10.

That’s one of the things that finally got me to decide that the Remen probably was 1.216733603 if the Great Pyramid model would “vouch” for it like that.

–Luke Piwalker

 

Palace of Vertical Grooves, Data Tables and Room 3 (PVG Pt 6)

I’m a bit in over my head with the Palace With the Vertical Grooves, with data flying everywhere but not complete models of rooms as yet and still a few mysteries, including whether we are looking at 5 Megalithic Feet or one of several Venus Synodic Period (VSP) values in places. The former would be classic but the VSP models seem to be have some things going for them, and it is Mayan architecture after all – so far its held up mathematically that there seems to be a premium on making reference to Venus.

The general pattern seems to continue that there may be a surprising amount of cross-referencing or self-referencing still taking place – the length of one room appears over in another room as the width or height or as a ratio, and etc.

As always, that in itself may indicate just how thoroughly and methodically these architectural designs were planned out.

Image

This is the most comprehensive data spread I’ve come up with so far. Some things are still missing. In orange table cells are my initial speculations on the possible original intended meaning of some of these measures – these are the numbers that figures that look the raw data often are or usually are. Little has yet gone into seeing if these proposed pieces of room measurements actually fit together sensibly.

Image

Image

I’m encouraged to think I might have understood correctly that the value of the vault diagonal (the diagonal of the vault face in the upper part of the room) of 926.3596784 cm = 30.39237783 ft may mean (30 / (Pi^2)) x 10.

One place this number has been seen before is that it has been proposed to be present in the measurements of the Aztec Tizoc stone as a significant facilitator to calendrical calculations

Tizoc Stone (Tenochtitlan) Diameter 2.60 m = 8.530183727 ft Thickness .88 m = 2.887139108
New Blood from an Old Stone by Emily Umberger
in Estudios de Cultura Náhuatl 28 (Instituto de Investigaciones Históricas, Universidad Nacional Autónoma de México
http://www.historicas.unam.mx/publicaci … 28/549.pdf
https://www.academia.edu/12232138/Umber … %C3%A9xico
“The monument is in the form of a cylindrical solid and measures 2.60 meters in diameter by .88 meters in height”
2.60 m = 8.530183727 ft = ?
.88 m = 2.887139108 ft = 2.882083037? Interpretation: Diameter = 8.760481938 ft – Radius = 4.380240969 ft – Circumference = 27.52186570 ft – Thickness (1) = 3.039635509 (30 / (Pi^2) ft – Thickness (2) = 2.882083037 f

Therein, we see it working to higher powers to connect some well known and important figures together, which connections allow the arrangement of measures to express these sets

8.760419838 / 3.039635509 = 2.882083037
2.882083037 x (3.039635509^2) = 2662.867198 = 7.396853328 / 360
2.882083037 x (3.039635509^3)= 1.61882914 / 2
2.882083037 x (3.039635509^4)= 18983.99125 x (360^2)
18983.99125 / 3.039635509 = 52.04568990 = “52” = 10.40913798 / 2
18983.99125 x 2.882083037 = 5.471343916 = (7.396853328^2)
18983.99125 x 2.882083037^2 = 4.380240969 x (360^2) = 1.216733603 x (360^3)
18983.99125 x 2662.867198 = 224.8373803^2
2662.867198 / 224.8373803 = 12 x (Pi^2)
224.8373803 / 3.039635509 = 7.396853328
224.8373803 / (3.039635509^2) = 1.216733603 x 2
224.8373803 / (3.039635509^3) = 16.01157243
(224.8373803^2) / (3.039635509^2) = 5.471343915
(224.8373803^2) / (3.039635509^3) = 360 / 2
(224.8373803^2) / (3.039635509^4) = (12 x (Pi^2)) / 2 = 365.0200808 / (1 / 1.622311470)
etc

https://grahamhancock.com/phorum/read.p … sg-1203988

So far, my experiments with the raw value for the length of the wall diagonal, 31.20822102 ft, suggest it may have been intended to be 31.22741393, the reciprocal of the powerful and important number 3.202314468, which is built into the Great Pyramid, and appears quite blatantly in my model of Mycerinus’ pyramid, where it appears as twice itself as the perimeter / height ratio.

My notes suggest that the combination of 31.22741393 and 30.39635509 would be a fruitful gesture generating series of modest length of useful numbers, largely by virtue of the significant if limited exponential value of 30.39635509.

A basic series generated from the two includes 4 x Venus Orbital Period, Lunar Leap Month, and the “Best Value” for the Eclipse Year, in rather direct and unambiguous fashion.

The vault height of 198 cm = 6.496062992 ft may be intended to be either 6.493939394 ft or 6.489245878 ft; 1 / 6.489245878 = 1.541011111 / 10^n, and this easy to remember number is thought to be part of the basic formulas for relating planetary cycles.

I am not certain which forms the best series with (30 / (Pi^2)) but 6.489245878 generates a series that might be more useful for being resplendent of the Egyptian Faiyum numbers, and 1.541011111 is itself 1/8 of the very powerful mathematical probe 1.232808888 = 2 / 1.622311470. Hence 25 / 1.6223114670 = 15.41011111.

However, it might even be some third number – I am not convinced by the ability of either 6.493939394 ft or 6.489245878 to form impressive series with (Pi / 3) or 2 Pi.

I am not certain what the floor diagonal of 921.746169 cm = 30.24101604 was intended to be although something that looks like this usually seems to be an “echo” of the Great Pyramid’s baselength of a suggested 3022.416640 ft, which is itself a simple multiple of the so far standard Saturn Synodic Period approximation of 378.09 days

3022.416640 / 8 = 377.8020800 (ft; 1ft=1day)

The width of the room, 180 cm = 5.905511881 is probably the simplest multiple of the Lunar Month, Lunar Month x 2 (29.53 x 2 = 59.06). Interestingly, the “Best Lunar Month” value does form a modest series with (30 / (Pi^2)) which includes the 9.712974840 figure that is still competing for a place in both Room 3 (see height of room, 296 cm) and Room 23 (see length of Room 23, 2.96 m), so again the sense of “interlaced” design elements.

At the minute I’m having trouble finding the formulas but the “Best Lunar Month” seems to appendage itself onto some important series.

The ratio between Room width and Vault width is 180 / 105 = 1.714285714, possibly a slightly distorted reference to Royal Cubit or Royal Cubit-like values? 105 cm = 3.44488189 ft itself tries to look like 2 Royal cubits but usually when we see the same number in the 2nd, 3rd and 4th places like that it’s probably a reference to the Eclipse Year.

The end diagonal of 11.36592043 (which resembles the Eclipse Year in meters) could be the Hashimi Cubit squared, or it could be twice the Bat Palace Wonder Number.

The room height / the height of the vault slope = 296 cm / 202.3023727 cm = 1.463156344, which we may have seen before in this most recent work on Tikal, and which is convincingly half of the “Real Mayan Annoyance”.

The 37.5 cm springline offset on either side of the vault in feet looks rather like some form of reciprocal Remen, possibly the variant involved in generating the Best Lunar Month, or a different one if they were content representing the “BLM” through the width of the room (see 180 cm / 2 in feet).

The length of the room I still find very mysterious (904 cm = 29.65879256 ft); it of course resembles the Lunar Month itself but the figure generally doesn’t go quite this high – 29.60881320 might be the maximum for the Lunar Leap Month and has the telltale ratio of 1.000723277 relative to the standard Lunar Leap Month of 29.58741331, which might be preferred for mathematical reasons.

It still remains to be seen then how most of these proposed parts might fit together as a whole, but I think the picture of Room 3 of the Palace of Vertical Grooves might perhaps be starting to develop nicely?

–Luke Piwalker

More Musings on the Palace of Vertical Grooves (PVG Pt 5)

Here again is the present data table with the basic data for the Palace of Vertical Grooves at Tikal (Tikal structure 5E-58, Group SE-11), collected from George Andrews’ report. I haven’t any further findings prepared but sharing some more of the ongoing exploration process might be informative for readers.

In the case of Room 1, I suggested that the length of 32.3162797 ft might represent 1/100th of the Lunar Apsidal Precession Cycle or Apsidal Cycle of 3233 days. The length / width ratio of 6.273885350 may well represent 2 Pi = 6.283185307 and the height has been suggested to be possibly 9.907871646 (this is half the value of a Pole or Rod in Inches, and yet this does refer to the same Pole used in Europe that may be a derivative of potentially older Indus Valley units).

The width would quite easily pass for 3 Egyptian Royal Cubits (1.718873385 x 3 = 5.156620155) but as previously noted there may be something strange going here in regard to the Royal Cubit that architects might have been deliberately opting for one or more similar numbers instead of the Royal Cubit per se for the purpose of their calculations and formulas.

We sometimes see similar things in Egypt, which may be potentially misleading to many people, but as I say when you work with a value extensively in the context of various data recording or retrieval schemes, you become aware of many numbers similar to but not equal to fundamental metrological values. I have occasionally referred to Teti’s pyramidion, which makes a good example. Hence the ancient Egyptians might easily have known a number of Royal Cubit-like values and have sometimes used them out of necessity.

However, I do not know of them having used Cubit-like values at the expense of the Royal Cubit. Whether the architect of the Palace of Vertical Grooves shared in that I could not yet say, but certainly there doesn’t seem to be readily available reason for contempt for the Egyptian Royal Cubit outright, especially since so many other Egyptian units seem to be on display in Tikal’s architecture.

Much of what I’ve been doing lately including lately including the ancient architecture of Egypt’s Faiyum region and several structures at Tikal seems to involve a unexpected rise in prominence and utility for the so-called Palestianian Cubit, which is essentially the diagonal to a rectangle measuring one Royal Cubit by one Remen, these two units quite possibly being ancient Egypt’s two most important measures.

In the previous post, I mentioned being tempted again by a possible Royal Cubit variant of 1.717631065. To be clear, I have thus far declined endorsing this as an actual ancient Royal Cubit value with what I believe is good reason. This might sound strange at first, but as tempting it is to endorse 1.717631065 as a genuine Royal Cubit value so the Egyptian Mystery Unit of 1.676727943 ft might finally be able to boast a historical identity as a form of such a variant Royal Cubit, the Egyptian Royal Cubit can already boast a key angular and matching square root relationship to the Egyptian Mystery Unit, and there might be something wrong with the idea of what might amount to trying to make a unit a diagonal to itself, if that makes any sense?

Another reason is another noble number 1.715917826 which might also have to be afforded Royal Cubit status on the same sort of merits, thus opening the floodgate to many other Cubit-like numbers. 1.715917826 may now also be leaping out from the design of the Palace of Vertical Grooves (PVG) to tempt me (which may mean that I should not be too quick to accept either one as anyone’s idea of a Royal Cubit).

If that is true that we may be seeing both 1.717631065 and 1.715917826 where we might usually expect the standard Royal Cubit of 1.718873385, perhaps what we are looking at isn’t the work of someone with contempt for the standard Royal Cubit value, but rather of someone with a particular fondness for Cubit-like constants who may have felt they were neglected and tried to include the design a few adept pointers toward their usefulness, similar to the sense we can get at Rio Bec of an architect who seemed to “take in stray numbers as if they were stray pets”.

The length / height ratio of Room 1 of 3.261589404 bears some resemblance to 1.2 Megalithic Yards (1 /100th of the outer circumference of the Stonehenge sarsen circle of 120 x 2.720174976 = 326.4209971 ft)

If I take the height of Room 1 to be 9.907871646 and the length / height ratio to be 3.264209971, the length projects as 9.907871646 x 3.264209971 = 32.34137342, which is easily close enough to 3233 / 100 that it could be a legitimate ancient expression for the Apsidal Cycle.

It’s a bit difficult to tell since approximations of the Apsidal Cycle and where they fit into the scheme of ancient astronomy formulas still isn’t entirely clear; so far there are only some experimental formulas based on various suggestions but not necessarily anything that seems to make complete sense so far.

If 32.34137342 i s the length of the room and the length / width ratio is 2 Pi, the width would be 32.34137342 / (2 Pi) = 5.147289446 ft. If we try to make 3 Cubits of 5.147289446, they would be Cubits of 5.147289446 / 3 = 1.715917826 ft rather than 1.718873385, so that is how 1.715917826 has found its way into the present discussion.

Like the ancient architect himself might have felt, I myself feel somewhat apologetic toward 1.717631065 and 1.715917826 for their having been so seemingly overshadowed by the standard Royal Cubit value. So far I haven’t seen the ancient Egyptians resort to substituting either one for the standard Royal Cubit value, and somehow in spite the merits and pedigree of both of these numbers, it’s been rare to not at all that I see them turn up in any proceedings.

I believe that my preference for the standard Royal Cubit value would scarcely explain the overall shortage of these numbers that I have seen in my work. Finding both in the Palace of Vertical Grooves might indeed indicate a theme of something of a “tutorial” on Cubit-like values.

So for now, I can’t consider a solution to have been found for the proportions of Room 1 of the PVG, and the only thing I can think to add to the discussion now is that 32.34137342 does not seem to be linked to any strong candidates for the Apsidal Cycle value by the ratios that would indicate the presence of a primary sent (A, B and C values) so the Apsidal Cycle itself also remains rather mysterious even after finding a surprising number of references to it in the architecture of Oxkintok in Mexico.

I might next point out that the calculated height / width ratio of Room 1, 1.923566879, may be similar to 1/2 of the calculated length / width ratio of Room 25 of 3.837500000. 3.837500000 / 2 = 1.9187. Number in this range may often represent the Half Venus Cycle (Calendar Round) / (Pi^3) and/or inverse approximations of the number 52, as in the 52 weeks in a year or the 52 years in a Calendar Round (52 x 365 = 18980, the canonical Calendar Round value). I don’t know that these are what was meant, but they are some possibilities to start out with.

Room 16, which shares a height of 3.02 m = ~9.907871646 ft with Room 1, has a calculated height / width ratio of 1.847682119, which may mean 1/4 of the Squared Munck Megalithic Yard, or (2.719715671^2 = 7.396853331 ft) / 4 = 1.849213333 although there might be some other possibilities including a simple fraction of the “Best Lunar Month” value. 4 Squared Munck Megalithic Yards may represent 1/4 of an idealized Lunar Leap Month, if 1/12th of a Lunar Leap Year: 7.396853331x 4 = 29.58741332 = 355.0489599 (Lunar Year = ~354 days + 1 = 355 days).

The length / height ratio of Room 20 calculates as 1.844444444, which is similar to the calculated height / width value of 1.847682119 for Room 16. 1.844444444 in Roo 20 has managed to attract the suggestion of possibly being 1.834791047.

Any or all of the occurrences of 1.80 m = 5.905511811 (Rooms 3, 4, 9, 19 and 20) that are suggestive of a simple fraction of the Lunar Year, could yet prove to be simple fractions of a Lunar Leap Year.

As often happens, with our scouting we may be getting some general ideas, although not necessarily exact ideas this early on.

There is perhaps yet another possible point of caution – perhaps not, but it might be best to mention it – which is that the value in the vicinity of 2.577142857 could also be potentially mistaken for versions of the Mayan Tzolkin period of 260 days. There are, not surprisingly, possible references to the Tzolkin that look even more suggestive, i.e., the 2.603351955 length / width ratio calculated for Room 12, which could prove to be the rather popular approximations 2.597575757. We seem to see both 2.597575757 x 100 and 2.602284495 x 100 in the sarsen and lintel circles respectively at Stonehenge and they probably remain our two best approximations of the Tzolkin.

2.597575757 might have been preferred because (1 / (2.597575757 x 2)) x (Pi^2) directly yields a viable form of the Calendar Round: (1 / (2.597575757 x 2)x (Pi^2) = 18997.2196 (Half Venus Cycle B) / 10000, which is not a property shared by (2.602284495x 2), which generates an HVC/Calendar Round only indirectly.

The length / height ratio of Room 11 calculated at 2.100323625, if taken most literally may be the rarely seen proposed short Palestinian Cubit-like (?) values of 1728 (12^3) Remens / 10^n = 2.012515666 if not a more conventional Palestinian Cubit value like 2.017038746 ft. The length of Room 11, 6.49 m = 21.29265092 ft, could perhaps be 21.34876318 ft = 20 Hashimi Cubits of 1.06748159 = 6.507103017 ft.

The length / width ratio of Room 28 calculated at 3.292517007 might turn out to be a case of the Meter-like figure of 3.289868134 (the so-called Guachimontones Meter), possibly just another occurrence of it in the Palace of Vertical Grooves if 3.289868134 proves to be a consistent meaning of the “1.01 m” width of Rooms 2A through 2C.

Returning to the subject of 1.717631065 and how it became part of the discussion, 1 / 3.881314681 = 2.576446597 / 10 and 2.576446597 / 1.5 = 1.717631065. There may really not be any indication we are meant to see 2.576446597 as 1.717631065 x 3. In fact, 3.881314681 and 2.576446597 have been part of the Tikal discussion since the very beginning, without 1.717631065 having to become involved.

For Room 14, length 14.79370666 / width 5.741903085 = 2.576446597 is certainly not unreasonable and may be a viable solution, and may actually display an important integration of ideas expressed in both Temple I and Temple II at Tikal.

For Room 22, the length of 7.85 m = 25.75459318 may also accommodate 2.576446597 x 10 into a sensible equation, where length 25.76446597/ width (2 Pi) ft = ratio 4.100542115, which has at very least some mild Wonder Number qualities to it and certainly deserves some consideration.

Here is some fresh mystery… I have two possible models so far for Room 23

Raw data (yellow row) and two possible models of Room 23 in the Palace of Vertical Grooves. The height / width ratio seems to be the reciprocal of 2 Pi.

I might have preferred to see the first version because of the 1.789199024 length / width ratio and the 9.733868824 ft length (1/10th of the inner sarsen circle diameter of Stonehenge) since 9.733868824 is probably a more useful number than 9.712974840, although the possibility of the later may be made more plausible if there is more dabbling in numbers associated with Temple I here, but the height in feet for this model, 8.286126829 ft is a bit unfamiliar, and seeing 8.268340458 might be preferred, but in the second model, the desirable figure of 1.789199024 is replaced by an unfamiliar number, 1.785358465.

Hence both proposals still seem a bit strange. As I was writing this, I went to apply a (Pi / 3) probe to see if I could it sort it out and be able to post a finished version, but I’m a bit astounded by the findings. The findings aren’t definitive, because both of the unfamiliar numbers look like Wonder Numbers that I don’t think I’ve ever seen before, or haven’t heeded before because I hadn’t found reason to.

Allow me a minute to try to find a short form to use to point this out

I might have preferred to see the first version because of the 1.789199024 length / width ratio and the 9.733868824 ft length (1/10th of the inner sarsen circle diameter of Stonehenge) since 9.733868824 is probably a more useful number than 9.712974840, although the possibility of the later may be made more plausible if there is more dabbling in numbers associated with Temple I here, but the height in feet for this model, 8.286126829 ft is a bit unfamiliar, and seeing 8.268340458 might be preferred, but in the second model, the desirable figure of 1.789199024 is replaced by an unfamiliar number, 1.785358465.

Hence both proposals still seem a bit strange. As I was writing this, I went to apply a (Pi / 3) probe to see if I could it sort it out and be able to post a finished version, but I’m a bit astounded by the findings. The findings aren’t definitive, because both of the unfamiliar numbers look like Wonder Numbers that I don’t think I’ve ever seen before, or haven’t heeded before because I hadn’t found reason to.

Allow me a minute to try to find a short form to use to point this out rather than reciting the entire series for them.

8.286126829 / ((Pi / 3)^6) = 2 Pi, and the series runs to about (Pi / 3)^10 and includes the Polar Radius, the Great Pyramid’s side length, and what is quite probably one valid representation of the Saros Cycle.

1.785358465 x ((Pi / 3)^5) = 224.8373808, Venus Orbital Period, another illustrious series that runs to about (Pi / 3)^10 or (Pi / 3)^11. That is very strange because it seems to mostly defy 2 Pi, but the VOP of 224.8373808 showing up in the series is obviously very important nonetheless.

At the same time, 8.286126829 also seemingly gives a muted response to 2 Pi in spite of a robust response to (Pi / 3) so that none of the most typical conserations seem to clarify which is really the better – and hopefully therefore the correct – proposal.

This also makes it harder to get a sense of the attitude of the architect – and perhaps it isn’t the work of any single architect – because some of the experiments imply the possibility of someone adept even with unusual numbers and who likes to make use of the knowledge, and some of them give the sense of a “classicist” who might be likely to do things a little more Munck’s way.

For Room 23, did the novelty of a length of 9.712974840, or the classic 9.733868824, (which is probably what Munck would have called it) prevail?

–Luke Piwalker

Design a site like this with WordPress.com
Get started