On the Great Pyramid’s Missing Apex

I know that I make frequent reference to the Great Pyramid’s “Missing Apex Section” – in fact, these passages from the very recent post “The Stars Built In” seem to make it particularly clear what my extended Munck model of the Great Pyramid implies in regard to the missing section:

I hope that by now, everyone understands what my model of the Great Pyramid actually represents. The origins of the extended model are simply that the height of the Great Pyramid as it currently stands was given by multiple sources as between about 452 and 454 feet; I originally proposed the value of 452.893421 feet purely because Carl Munck held this number in such high regard, referring to it as a “Holy of Holies” and I though this interpretation might make him happy.

It was only some time later that I realized myself more about what I was looking at, that this gesture had created a ratio of 1.718873385 x 10 – the value of 10 Morton Royal Cubits in Imperial feet – as the ratio between the whole pyramid and the part now missing.

In other words, I’ve been seeing this “unit value in Imperial measures as ratio” phenomenon since the very beginning of my Egyptological studies, and last saw it as recently as my last Egyptological study, where we find Remen in Imperial as ratio in the data from Mariette for one of the coffers in the Saqqara Serapeum, the ratio between the coffer’s inner and outer length, or even from the raw data, 3.85 m / 2.17 m = 1.214511041 = ~1.216733603.

How do we justify this assessment of the Great Pyramid’s missing section? If we look at the Great Pyramid in its present condition, there is almost 28 feet missing at the top, and yet from bottom to top we see it stripped only of the prized casing material, implying that there was a definite cut-off point some 28 below the projected apex with the pyramid above theis level made of a different material that supported the actual capstone. I would quite be surprised if the capstone itself exceeded 7 feet in height.

Frequent reference has also been made to how the numbers from this projection of the missing section turn up in a great many other places (including Stonehenge, for example in the mean proportions of the sarsen circle), and how astronomical data can easily be recovered from the missing apex section in spite of its absence.

In spite of all this, relatively little may have been offered recently in the way of demonstrations of this.

How about we begin at the beginning briefly?

If we take Munck’s height for the Great Pyramid (from the presumed pavement level) of 480.3471728 ft, and subtract from it the projected height at which the transition in materials is proposed to take place, 452.3894321 feet, we obtain the missing apex section’s height projection of

480.3471728 – 452.3894321 = 27.95783074 ft.

The interpretation of this figure is given as 27.94546572 ft, which is accurate then to 27.94546572 / 27.95783074 = .999557725. This is the first time the “Giza Standard” of accuracy on approximations of geometric necessity of .9995% or higher was seen in action.

If you find any of Michael Morton’s work on the Internet, or some of my older writing, you may see the number 27.94546572 referred to as the “LCS” constant. We were working with the idea that three serpent-themed monument including “Le Serpent Rouge” in France and a purported Scottish serpent effigy made of stone, were capable of holding a sort of “geomathematical conference” in which they were able to collectively generate this number, so we were aware of the number and some of its properties even before its rather astonishing appearance in the Great Pyramid.

Most of what has been learned about 27.94546572, however, has come after my realization of the ancient imperative to record astronomical data in monuments.

With a perimeter / height ratio for the Great Pyramid of 2 Pi, this height x 2 Pi = 27.94546572 x 2 Pi = perimeter 175.5865396 ft for the missing section.

Because this in itself sets up the ratio of 10 Royal Cubits in feet = 1.718873385 x 10 between the whole pyramid from the pavement and the missing section, no one thought to try converting these specifications for the missing apex into Royal Cubits – we’d already done that, it seemed – but that is another discovery from more recent years that we can use the Royal Cubit value that way as a mathematical probe, to retrieve some important numbers, including some of the “Mayan Wonder Numbers” from the Tikal temple pyramids in Guatemala.

So, even though the total projected height of the Great Pyramid from the pavement in Royal Cubits is already 480.3471728 / 1.718873385 = 279.4546573 Royal Cubits, we can still make a meaningful conversion of 27.94546573 feet to Royal Cubits, so that the height of the missing apex in Royal Cubits would be

So, even though the total projected height of the Great Pyramid from the pavement in Royal Cubits is already 480.3471728 / 1.718873385 = 279.4546573 Royal Cubits, we can still make a meaningful conversion of 27.94546573 feet to Royal Cubits, so that the height of the missing apex in Royal Cubits would be 27.94546573 / 1.718873385 = 16.25801294 Royal Cubits.

For a minute, we might puzzle over them not having managed 16.22311470 ft since this is one of the numbers that ancient architects seem to have wanted to build into everything, but what 16.25801294 is, is the reciprocal form of one the “Mayan Wonder Numbers”, and is in fact also 1/18th of another “Mayan Wonder Number” – none other than the dreaded “Real Mayan Annoyance”

292.64422329 / 18 = 16.25801294, so from the conversion to Royal Cubits, we only need to apply half of 360 (as in 360 / 2 Pi) in order to find the astronomically significant “Real Mayan Annoyance”

360 is one of the very first numbers that the Great Pyramid should make us think of, because of the role of 2 Pi in the geometry of circles.Virtually every number we can find in the Great Pyramid may respond to 360, 2 Pi, the Radian, or all of them, by releasing at least one stored significant data point. We also use 2 Pi to derive the same version of the Royal Cubit from whole numbers, that is embodied by the ratio between the missing apex section and the whole.

I very strongly agree with what Carl Munck said about the Great Pyramid – that its primary mathematical identify is as “a three-dimensional model of the number 2 Pi.”

For those who might be tuning in late and haven’t had the chance to read some of the older posts, the “Real Mayan Annoyance” was given such a preposterous name because it created considerable confusion at times whether we really seeing 2.926442329 or 2.920160646.

I had just found 2.920160646 at Tikal in proper context, and I thought, “Fantastic! The Maya knew this Egyptian number too. This will be easy then, because just like Egypt, every time we see “2.92-something” we will know it’s 2.920160646″ – and I of course was greatly annoyed when I first discovered that this was not so, and identifying “2.92-something” was going to be ten times as much work as I expected.

For those curious, let me take a minute to explain “proper context”.

.

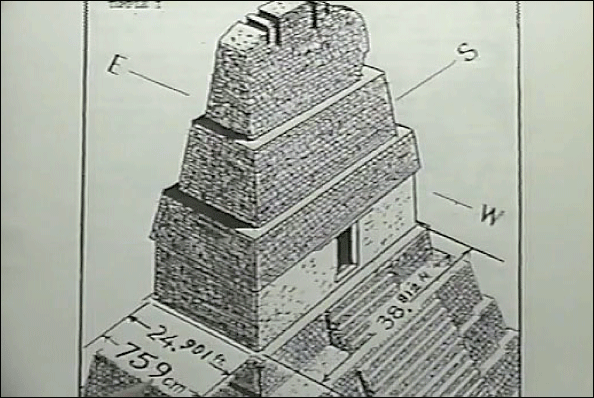
Munck’s own drawing of Tikal Temple I labelled with Maler’s data and conversions from meters to feet, from http://www.viewzone.com/bigpicture/bp112311.html.

Both the width and length of the Temple platform of Tikal Temple I are geodetic figures, and the width value could not be a more blatant one, using about 24.901 ft to represent 24901 miles equatorial circumference. We could think this just coincidence, but the length is an almost insanely clever second geodetic figure, and Maler’s data also shows us that the very same thing happened, only in reciprocal form, atop the El Castillo Pyramid at Chichen Itza.

We also have it on good authority that the width of Tikal Temple III is 890 cm = 29.19947507 feet.

Hence in this case at least we can be fairly certain that we are looking at 29.20160646 and not the dreaded “Real Mayan Annoyance” 2.926442329 x 10, because the situation is that while we have what is probably 24901.19743 displayed atop Temple I is as blatant a manner possible (and in “modern British feet” no less), atop Temple III is an equally blatant display of the very same number in cube root form!

29.20160646^3 = 24901.19742

From there, 2.926442329 is the “Real Mayan Annoyance” because there turned out to be a half dozen very similar numbers that exist within Munck’s mathematics that are apparently considerably less rewarding to get involved with.

Going back to the Great Pyramid’s missing apex section, if we convert its perimeter into Royal Cubits (27.94546572 x 2 Pi = perimeter 175.5865396 ft), 175.5865396 / 1.718873385 = 102.1521080 Royal Cubits, and 102.1521080 is another “Mayan Wonder Number” – also from Tikal, where we find it at the top of Temple IV. It belongs to what is still one of the most powerful and fruitful (Pi / 3) series I have ever seen, as was discovered because the Mayan architect actually seems to have combined it there with (Pi / 3) x 10 feet as another of the proportions of the same doorway.

So all of that comes in to play just in the conversion of the height and perimeter of the missing apex section into Royal Cubits!

The basic metrological unit of the height of the missing section is the Egyptian Mystery Unit phrased as 5 / Egyptian Mystery Unit 1.676727943 ft, which is to the Mystery Unit value what 1.067438159 is to the Egyptian Royal Foot – a frequently more useful form. 167.6727943 / 6 = missing section height 27.94546572 ft.

As it turns out even with little if any a priori knowledge of astonomy or ancient calendars at the time it was first proposed, if we follow along with the logic that because there Giza is dominated by a pyramid that is a massive advertisement for 2 Pi, that we should try throwing 2 Pi at every number we find there, creating a pyramid with an upper section of this height turns out to be quite a desirable goal for anyone wanting to express important numbers from astronomy (or geodesy).

Let’s now being the roll call…

Temporarily ignoring correct decimal placement, which is inconsequential here

27.94546572 / (2 Pi^1) = 4.447659006 = 1 / 224.8373808

At the very first power of 2 Pi, the projected missing height of the apex has responded with the Venus Orbital Period, in its primary form – its most useful and important form.

27.94546572 / (2 Pi^2) = 7.078669160 = 353.9334580 / 200

At the second power of 2 Pi, the projected missing height has given us twice the standard value for the Lunar Calendar Year, with 353.9334580 approximating “354” days. This is still the most useful representation of the Lunar Year that I’m aware of.

This downward progression with useful numbers (some in reciprocal form) as output continues down to

27.94546572 / (2 Pi^7) = 7.228568039, which is the reciprocal form of the revised perimeter of Menkaure’s pyramid, “G3”, itself a measurement with both geodetic and astronomical function because the very important Hashimi Cubit is the root of it in sensu Petrie (whole number of units): 360 x 360 x 1.067438159 = 1383.399858 revised G3 perimeter = 1 / 7.228568039. I wouldn’t know 7.228568039 on sight myself but a simple reciprocal check of 1 / “x” reveals what it is.

At 27.94546572 / (2 Pi^9), we find the reciprocal of 54614.43732, which is 2 x 360 x 360 Palestinian Feet. It doesn’t seem to be often used but its significance is recognizable.

Beyond that things get a bit strange so we will demarcate that as as territory to be avoided.

In the upward direction 27.94546572 x (2 Pi^2) = 110.3247266, which is our best Eclipse Year divided by Pi.

110.3247266 x Pi = 346.5939368

That is at least ten important pieces of data recovered, including the Venus Orbital Period, Lunar Year, and Eclipse Year, just by applying the ratio 2 Pi to 27.94546572 value actually found atop a 2 Pi pyramid.

If you run the progression yourself, on the way down you will meet what looks like half of the “Not Venus” number. Pay no mind to that, as we’ve already found the true Venus Orbital Period at the start of the downward series. What the number really is, is the reciprocal of the square root of the generic volume of a sphere.

The reciprocal of Munck’s Giza Vector Number is in there too, which is also an astonomy-related number, including that is square was apparently used in ancient reckoning of time.

360 will pull 3 more important pieces of data from 27.94546572, and the Radian value 57.29577951, at least four more. Now at 17 pieces of important data just from putting 27.94546572 atop a 2 Pi pyramid. That of course isn’t the crown jewel of the pyramid, that’s just what the crown jewel rests on.

None of this yet touches on the fact that the projected missing section was also found to have significant base diagonal, vertical edge, and slope length. The base diagonal length as determined by ratio to the whole (that is, the base diagonal of the whole pyramid divided by 10 Royal Cubits in feet) is a geodetic figure related to the polar circumference in miles by 360 as a ratio.

Were it only that we could make the corresponding projection for Chephren’s pyramid, I presume we might see something equally splendid, but sadly I still no have reliable data on the current height of “G2”, and while there is some data from Maragioglio and Rinaldi that may even include corroboration of a platform height established well below the base of the capstone just as we would want to predict, I have not been able to obtain the vital parameter of either height of the present platform or the length of its sides, in order to perform the calculations.

Unfortunately, I also have little faith at present in historical sources (there is more than one) that amazingly, claim to offer dimensions of the Great Pyramid’s original capstone.

Likewise, Petrie’s data avails us little corroboration of the Great Pyramid’s present height. His course heights are different at different corners, and even if we somehow miraculously added them all up without generating egregious cumulative error, there is still the matter that the surviving top course may represent merely the protrusion that fit into a formed socket in the base of the missing section, meaning that its height cannot be expected to assuredly be at the same height on the pyramid as the base of of the section that’s missing.

These specifications for the missing section have now stood for at least 15 years without anything prompting a revision – even when I ask myself on a daily basis, “Am I sure I have this right?”

Maybe someday we will learn how to know more of the story.

In the meantime, we can continue to throw more power probes like sqrt 60 or reciprocal of sqrt 60, or 1.177245771, or 1.622311470 or 2 / 1.622311470 at the proportions of the missing section to secure even more important data, further adding to our knowledge of the Great Pyramid’s encyclopedic collection of important data.

–Luke Piwalker

A First Look at Hadrian’s Library

Athansios Angelopoulos, author of Metron Ariston, has provided us with plans and data for (among other things) Hadrian’s Library. I have not looked at much the material carefully yet, but already there may be several things worth mention.

Says Wikipedia,

“Hadrian’s Library was created by Roman Emperor Hadrian in AD 132 on the north side of the Acropolis of Athens 

The building followed a typical Roman Forum architectural style, having only one entrance with a propylon of Corinthian order  a high surrounding wall with protruding niches (oikoi, exedrae) at its long sides, an inner courtyard surrounded by columns and a decorative oblong pool in the middle. The library was on the eastern side where rolls of papyrus “books” were kept. Adjoining halls were used as reading rooms, and the corners served as lecture halls.

The library was seriously damaged by the Herulian invasion of 267 and repaired by the prefect Herculius in AD 407-412.”

Thus we may ultimately have some questions about how the proportions described by Angelopoulos came to be, but for now let us take a closer look at a few of those proportions themselves.

To be honest, I am not quite certain what to make of the figure 82.75918635 ft. I think it may be noteworthy that some of the figures here are more that may be capable of tricking us if we are not aware of the possible imperative to reduce the pool of available whole numbers in order to ward off metrological chaos.

The truth may be that even a single metrological unit used with even such a restricted pool of whole numbers can be enough to create confusion that requires us to look for secondary means of confirmation.

At any rate, what I would most like to showcase here at the moment is the length and width of the complex made of the library and the two adjacent auditoriums. In Imperial Feet these are 266.8799213 and 58.80905512 respectively.

By now, these are hopefully very readily recognizable as

266.8799213 x 4 = 1067.519685 = ~1000 Hashimi Cubits 1067.438159, and

58.80905512 x 2 = 117.6181102 = ~50 Megalithic Feet = 50 x 1.177245771 = 58.86228855.

If these are the intended figures, the overall length / width ratio would be

(1067.438159 / 4 = 266.859398) / 58.86228855 = 4.533624946

That’s a bit unexpected – it might be more comfortable had it come out 4.523893421 for example, but technically the figure is ten times 1/6 of a Megalithic Yard of 2.720174976; thus it may be an acceptable figure whose “reason for being” remains for the moment better known to the architect than to ourselves.

We might assume that if 4.533624946 is the intended figure, that it was considered acceptable because it has some significance to astronomy, as do the elements it is constructed from here. It takes only a few simple calculations to see that this actually does appear to be the case; furthermore, the products of the library complex’s length and width also possess astronomical significance.

These do not give us the true area of the complex since the diagram shows the library extending out further than the auditoriums, but it does provide us with mathematically and astronomically significant figures.

Let’s look at the auditoriums for a moment. If they are designed symmetrically to be equal at both ends, they should have interior of length 16.1 m and width 14.26 m. Since we don’t need to convert units to check ratios since ratios will remain the same regardless of unit, we can use the metric figures to estimate the proportions of the rooms 16.1 / 14.26 = 1.129032258.

This figure, impossibly large to be 1/200 of any sensible approximation of the Venus Orbital Period, nonetheless equates to 400 / 354.2857143, a very good approximation of the ~354.36 day Lunar Year.

We note that some may wish to interpret the raw value of 52.82152231 as related to the 5280 foot mile or to the Indus Foot of about 5280 / 4800 = 1.1; to keep to our experimental assessment, the raw calculation for square footage of one or both the auditoriums given the data available is

52.82152231 x 46.78477690 = 2471.243137 = 4000 / 1.618618557.

This is presumably referring, if the data is accurate, to the form of Phi that was extracted from the Great Pyramid by means of close approximation and actual in situ use, namely our friend “Not-Phi” 1.618829140.

From here, given certainty about the identity of 46.78477690 ft, we might back calculate the true intended value of 52.82152231 ft. I am not quite certain what 46.78477690 is meant to be.

Those familiar with Munck’s materials know that 46756.36369 (1.718873385 x 2.720174976 x 10^n) was a number he associated “geomathematically” with the pyramid of Menkaure (Mycerinus); 48 Roman feet would be 48 x .9733868822 ft = 46.72257035 ft = 384 Egyptian Remens.

Once again, ancient metrology can become overpopulated with similar figures even with a drastically restricted pool of whole numbers such as I am using, and we are reminded of that again here already because in spite of those two glittering possibilities, we may also wish to to note that 5 / 1.067438159 = 46.84112103 / 10^n, 46.78477690 x 45 = 2105.314961. Thus we could also be seeing Hashimi Cubits again, or Palestinian Cubits respectively.

The latter may make a little more sense if what is emerging is a pattern of someone opting to use a palette of typical units.

If that is the case, we might expect to find next perhaps the Megalithic Yard or the Egyptian Mystery Unit, or perhaps Indus Units.

Indeed, 92.06036745 could be in Indus Units (92.06036745 x 12 = 1.104724409 ft x 10^n) and 82.75918635 could be in Megalithic Yards (225 / 82.75918635 = 2.71831417), which actually resembles the version of the Megalithic Yard that can be constructed from the Harris-Stockdale Megalithic Foot or something very much like it such as 1.177245771.

Its a bit unusual, but 52.82152231 x 2304 = 1.217007874 x 10^n, which could be in Remens. 82.75918635 could also be a display of the Egyptian Mystery Unit in Inverse form: (1 / 72) / 1.676727943 = 82.83328817.

This is not necessarily an easy puzzle even when we may be able to see the theme of the choices of measurement.

The ratio between the length of the Library and of the auditoriums is 28.06 m / 25.225 m = 1.112388503 = ~250 / 224.7416251, which looks very like the very typical backhanded tribute to the Venus Orbital Period that we see so much of. Hopefully then if we manage to identify either 28.06 or 25.225 in feet, knowing this ratio might be will allow us to know what both values really represent.

The ratio between outer length of auditorium and reading room combined (28.06 m) and inner length of auditorium (16.1) is 28.06 / 16.1 = 1.742857143. As a length measure, this would most likely be in Egyptian Sacred Cubits since we can perfect the estimate as sqrt 4860 / 40 = 1.742842505 and we have learned that valid square roots of whole numbers are in practice the essence of the Egyptian Sacred Cubit (see also Thom Mid-Clyth Quantum), while in origin the Egyptian Sacred Cubit seems as it may be be Remen x Royal Cubit, using their values in “modern” feet.

I think I will leave it at that for a first look. Once again, I hope we have made some important inroads with the particular subject even if it may be a particularly challenging design to interpret.

–Luke Piwalker

A Few Curious Notions

The Folkton Drums

Something I have been working on the past several days besides ancient Greek architecture is the Folkton Drums.

Thanks once more to researcher Geoff Bath for putting another interesting subject on our radar. Geoff informed us that the Folkton Drums are the subject of a final chapter of his latest book, and I am delighted to think this may mean we can expect this latest work of his relatively soon.

I have been looking at the designs on these artifacts and it occurs to me that we may be seeing multiple graphic ways of representing the 2:1 rectangle and its internal geometry, the Vesica Piscis, which in the post before last, I have pointed out yet again serves to coordinate a number of ancient units of length measure.

Are those fish scales on the possibly Vesica Piscis-derived diamond in the detail at bottom left? These possible Vesica Piscis seem as if they may remarkably geared toward ichthyomorphic (having shapes characteristic of fish) expressions for something of their purported antiquity.

The Folkton Drums have been making the news the last several years because of the efforts of Mike Parker Pearson, Andrews Chamberlain and Anne Teather, who have proposed that the drums were used to measure out measuring cords in Long Feet, a unit that Pearson and Chamberlain have championed in spite of some remarkable implications.

One is that their proposed unit value of 1.056 ft = 1/5000th of a 5280 mile exactly. One wonders if Peason and Chamberlain are aware of this, and that because of it, their campaign for the Long Foot also represents something of a campaign suggesting that the 5280 mile and the Imperial Foot are older than Stonehenge.

I have no disagreement with that basic premise, but then again I’m on the further outskirts of “fringe research” whereas they are ordinarily very respectable orthodox archaeologists and academicians and I’m still rather surprised to find them dabbling in ancient metrologies that imply everything we think we know about the origins of the foot and the mile may be little more than sheer fabrication.

I am also tempted by all this to wonder if their eagerness to adopt such a heretical cause may imply that their generally dismissal of Thom’s Megalithic Yard may be somewhat in haste.

Meanwhile, back on “the fringe”, researchers such as Jim Wakefield and DavidK have known for some time that the Long Foot of 1.056 can be equated with the Indus Foot of 1.1, the European Rod, and etc (5280 / 1.1 = 4800).

I use a slightly different value for the Indus Foot, mainly 1.100874623 ft, which equates the Indus Foot to the Megalithic Foot rather than to Imperial, because this is one of the curious things that the design of Stonehenge seems to urge us to consider, along with no less than two additional Megalithic Yard values which are also based on the Megalithic Foot, as I’m sure I’ve written about before often when discussing Stonehenge.

I’ve personally never been comfortable with the idea of a mile of 5280 feet exactly being anything more than an Imperial-based reference unit reserved for unit conversions such as the number of miles in earth’s circumference; some may find the number appealing because it’s easily divisible by 11 as was just demonstrated, but it’s still not easily divisible by 7, 13, 17, 19, or a host of other while whole numbers popular with other researchers.

Either way, we may be able to push the origins of Imperial measures quite a ways back than usually given credit for.

At any rate, if I indulge Pearson and Chamberlain with the notion of the Long Foot and make the short side of 1/4 of 1:2 rectangle to be 1 Long Foot = 1.056 feet, the diagonal (sqrt 5 to the short side) looks like the Ubaid Cubit, rated by its academic proponents at about .72 cm.

As far as I’m concerned, the Ubaid Cubit is still only an experimental unit, and one for which I have yet to find any definitive or primary value, and one of the most promising examples of its possible use is the division of the Great Pyramid perimeter at the base into 1280 Ubaid Cubits, at the same time this base perimeter has already been reckoned by a growing number of sources including John Michell (in View Over Atlantis), Hugh Franklin, and myself as consisting of Inverse Megalithic Feet.

However, the subject has come up before as I tried desperately to plot the origins and nature of the problematic 5280 foot mile; at least once before it’s been lost in the shuffle, but since the Ubaid Cubit is rated at 72 cm, making it a value in Metric, and the Long Foot can be qualified as Imperial, this exercise highlights an apparent sqrt 5 relationship between Imperial and Metric that can be difficult to dismiss as sheer coincidence.

Perhaps it’s time to begin treating the subject more as if it isn’t coincidence.

“Out There”: The Outer Sarcen Circle Diameter Unit and the Egyptian Mystery Unit

I continue to struggle to try to give historical names to several by now well established metrological units or simple multiples or dividends thereof. These probably aren’t new ideas on my part either, but they do come to light again in the proceedings.

One, is that the Stonehenge “Outer Sarcen Circle Diameter” value and its kindred like the height of the Great Pyramid from the base and the standard value used herein to approximate the Jupeter Orbital Period, which has been proposed to possibly derive from an oversized Assyrian Cubit that comes with its own rules opposite the usual when it comes to conversion into Remens, was actually featured in Teti’s pyramidion, whatever the true identity of the unit is.

Teti’s pyramidion, based on the available data, is a particularly good example of the metrological focus that may often be seen in the reported measures of pyramidia (pyramid capstones), with the data clearly indicating a rectangular base of 1 Royal Cubit long and 1 Remen wide.

It has been proposed that in this pyramidion, the standard Royal Cubit has been substituted for by the cubit-like value of 1.731717175 ft as a bridge between the Hashimi Cubit and standard Assyrian Cubit (1.731717171 / Hashimi Cubit 1.067438159 = Assyrian Cubit 1.622311470 = 1.5 Remens) where the standard Royal Cubit is not able to fulfill this function, even while the standard Royal Cubit value can be found in the base length of the very same artifact.

To me, it comes as a relief that we are less obligated than ever to try to pass off 1.731717175 as some sort of Royal Cubit once we learn what it really is. It appears that when the designers of Teti’s pyramidion were assembling a phenomenal collection of ancient metrological unit values in a single artifact, they didn’t overlook the “Outer Sarsen Diameter” unit.

At Stonehenge we see the mystery unit as diameter 51.5151515 ft – (circumference 120 Megalithic Yards of 2.720174976) / Pi = diameter 51.95151515 feet (and we have some recent revelations about the role of numbers like this in geometry thanks to fellow researchers); at the Great Pyramid we see it as the height from the base of 481.0325483 ft

I’ve been trying to make it point lately to mention more often that 51.95151515 / 481.0325483 = 108 / 10^n (the same relationship as between Hashimi Cubit and Egyptian Royal Foot); thus they are cut from the same unit, whatever it actually is.

481.0325483 / 1.731717175 = (1 / 360) / 10^n and 51.95151515 / 1.731717175 = 30.

Thus the value 1.731717175 ft not only isn’t a form of the Royal Cubit as far as I’m concerned, but it doesn’t have to be a Royal Cubit, especially since it’s already busy being a value in “Outer Sarsen Diameter” or “Great Pyramid Height” units.

Curiously, the next item is somehow in a similar vein and concerns the seemingly perennial quest for the historical identity of the “Egyptian Mystery Unit” or “LSR” of 1.676727943 ft. Proposals have been made that it may it be related to the Indus Foot (Jim Wakefield) or that it is a form of Sacred Cubit, but it was the failure of this unit value to slot into the John Neal-like array of unit values I was working on that just about tanked that scheme, and it may be the general awkwardness of the whole array that will manage to keep it tanked.

Previously, I’ve been called upon to give some thought to the possibility of several other Royal Cubit values, but the frequency with which they are mentioned (hardly ever) should already tell us that these “alternate cubits” are probably about as useful as the proverbial “screen door in a submarine”, in spite of some interesting pedigree.

One is 1.715917826 = ((1 / 1.6188249140) / 360) x 10^n; the other is 1.717631062.

What 1.717631062 is, or one way of expressing it, is the Morton Cubit / the most important very fine ratio 1.000723277: 1.718873385 / 1.000723277 = 1.717631062 – but this may not be a good direction to go in because the affinity of 1.718873385 for 1.000723277 generally seems to be in the upward direction (and “as a rule” it seems to be generally one or the other but not both with units modified by 1.000723277), with 1.718873385 x 1.000723277 = 1.720196697, which is a way for us to approximate and represent 1.216733603 x sqrt 2 = 1.720721163.

Readers may recall that this is because the relationship between ideal Royal Cubit and ideal Remen is not really sqrt 2, such that the true diagonal to a pyramid in Morton Royal Cubits is actually in short Remens standardized to (12 / Pi^2) feet each, and not the long Remen of 1.216733603. It would not be worth sacrificing either 1.718873385 or 1.216733603 to make it work out otherwise, not at all.

This may prove to be a very reckless suggestion, but with both 1.618829140 and 1.622311470 x 1.000723277 = 1.623484851 (possible root unit of the “Outer Sarsen Diameter” value: 1.623484851 x 32 = 51.9515151) emerging as possible variants of the Assyrian Cubit of 1.622311470 ft that may come with their own rules about not trying to convert them to Remens as we would the the standard Assyrian Cubit, perhaps it’s possible that 1.676727943 qualifies as a variant derivative of the standard Royal Cubit (rather than a derivative of a variant Royal Cubit) that comes with its own unusual rules about not back converting it into Royal Cubits?

I apologize for that rather convoluted looking proposal but hopefully my metrology still isn’t half as strange or complicated as John Neal’s. The lack of historical identification of 1.676727943 really has gone on for far too long not to turn every stone possible in search of the answer.

For what it’s worth, the equivalent to 288 / 1.717631062 = 1.676727943 x 10^n using Morton’s Cubit would be 288 / 1.718873385 = 1.675516082. It’s curious that we don’t see this number once in a while – not because I am always turning it into 1.676727943, but rather it just doesn’t seem to fit anywhere while 1.676727943 fits in many places and has many important roles – because it’s really not more exotic than (Pi / 3) x 16 = 16.75516082.

Given that ornaments from Chichen Itza frequently show division of a circle into 16ths, and we can readily fathom the relationships between the number 16 and the Venus Orbital Period, I’m really somewhat surprised that I cannot seem to remember emerging from any proceedings there.

This is even more strange because where we would use 1.676717943 with Pi to generate the A version of the Calendar Round: Pi x 1.676727943 = (1 / 18983.99126) x 10^n, we could use 1.675516082 analogously to generate the B version of the Calendar Round: Pi x 1.675516082 = (1 / 18997.72195).

What is more – I was about to say that 1.675516082 with Pi^n probably generates an unwanted junk series, but the fact is that 1.675516082 with Pi^n generates a useful and familiar, if very modest, series which includes 51.9515151.

It may really be only semantics anyway, but one reason I’m still very hesitant to accept any of this is because even if there is some variance in the equations, there are so many pointers to 1.676727943 metrologically that I still would expect it to have a novel identity of its own, if it cannot achieve equivalency with any already established major unit.

The Stonehenge “Oval With Corners” Unit Still At Large

There is another metrological mystery still afoot, which is the fundamental metrological unit of the Stonehenge Bluestone “Oval With Corners”.

After years of thinking it was going to turn out to be probably (1 / 12) x 10^n = 138.8888888 or maybe 1.177245771^2 x 10^n = 138.59070605, the value settled on as the likely value of the Stonehenge Bluestone “Oval With Corners”, 138.6375741 ft, came as a last minute surprise.

It’s a number that may have some strange properties but by now it has hopefully been rather well tested. It’s important because it’s a simple multiple of the ideal Eclipse Year value, and it quickly accumulated pedigree when under study with multiple metrological pointers to it – readers might happen to recall that the ideal Eclipse Year value can also be fashioned from the Megalithic Yard and Megalithic Foot, therefore so can the “Oval With Corners Number” 138.6375741

(Megalithic Yard 2.720174976 / Megalithic Foot 1.177245771) x 15 = ideal Eclipse Year 346.59939339 / 10).

It’s still a tricky figure, though, because since it didn’t turn out to be 1.177245771^2, it’s ended up as the freakish contraption 1.177245771 x 1.177643424. The trick here is of course to not divide it by 1.177245771 if that’s going to generate nonsense, but to multiply it by 1.177245771, repeatedly, which generates a nice little series that goes at least as high as 138.6375741 x (1.177245771^6) = ideal (“Best”) Lunar Month / 8.

Perhaps it’s a bit odd because it has (1.067438159^2) x 1.216733603 in its pedigree – another combination of fundamental Stonehenge metrological units we can build it from, but the incorporation of a square like that is unusual.

(138.6375741 also has some other aliases related to important components of Stonehenge; for example (51.95151515 / 1.177245771) x Pi = 138.6375741).

Again though, the “Oval With Corners Numbers” does have some unusual mathematical properties; for instances it tries to trick us into thinking it’s 1/49 of the Nodal Cycle or ten times 1/495 of the Saros Cycle, both 49 and 495 being numbers we know do not actually belong to our vocabulary.

It’s simply a very novel number that has become associated with a very unusual Megalithic construct. It’s status as 4 x ideal Eclipse Year is reason enough to put up with it.

So even for as far as we’ve come, we may still have a slightly incomplete picture of ancient metrology, but I like to think it isn’t for lack of trying.

Maybe someday?

–Luke Piwalker

The Stars Built In

I have no real explanation for why ancient people were such fetishists for astronomy. Were they that much believers in astrology and horoscopes? Did they have a religious belief that building numbers from calendars or decimal numbers that carry out for forever like Pi or 1.333333333… into their architecture meant they were building the imperishable cycles of the heavens or of mathematical eternity into their works?

Perhaps there was some other purpose that we have yet to understand, such as some link between calendar cycles and potentially catastrophic events such as droughts, that led such a phenomenal preoccupation with astronomy – or perhaps it’s simply as I’ve suggested before, the stars in the sky were what there was to watch at night before there were “stars” on TV.

Maybe we are still begging for explanation that we already have. In a way, there is enough of a purpose in all this just in the use of the stars or planets for purposes of navigation by night, a concern that has probably become dimmer for us now with every new streetlight and each advance in electronic navigation.

What is clear is that these concerns did not evade the concerns of metrology; quite the contrary, one major ancient unit of measure after another has been shown to have a value in Imperial measures that is quite prominent in basic calculations of multi-body calendar system, as has often been discussed in considerable detail here.

This happens with such frequency that it is less and less of a leap of logic to assume that these ancient measures began with astronomy, and even that accurate metrology was probably originally created as a way of writing down these calendar values is a universal language that can exist independently of the written word, which may help to explain the rarity with which these important operations were written down in textual form (as may the durability of the architectural medium as a vehicle for storing such data).

Because of these relationships, we can scarcely apply 1 Remen, let alone 3, without making reference to the Solar Year, or 1 Royal Cubit without making reference to the ratio Solar Year / Lunar Year, which may suggest to some that all of this was incidental if one cannot use a value of 4 Royal Cubits without making reference to the cycles of Mars or etc, yet it is much more difficult to believe there is anything incidental about these relationships in terms of their roots and origins.

To put it somewhat more casually, “Okay, so maybe they didn’t mean Mars every time something measured 4 Royal Cubits wide, but how on earth did they end up with units with values that could even have us asking this question in the first place?” – which is why I find a number of my working assumptions more or less unavoidable, no matter how we try to look at it.

The ancients very much seem to be eager to talk about astronomy, and they seem to have a great deal to say on the subject.

To put it another way – yes, they are constantly referencing astronomy with simple applications of common units and more or less unavoidably so, and if they did not wish to do so, they should and could have have simply chosen different units. They did not; instead they held onto these unit values as if they were consciously preserving what they believed to be the very oldest mathematics.

There is little saying they were not aware of this, and there is little blaming it on “coincidences” involving the Imperial Foot. Finding a unit value for reference that would give all these splendid astronomical meanings to ancient units must be harder than literally finding the proverbial needle in the proverbial haystack., the sort of “coincidence” that is engineered long before it ever happens by chance.

The much greater likelihood would seem that this most magical reference unit, the so-called Imperial Foot, has been with us since the beginning, and there are at lest three or four mathematical schemes that stand in evidence of how and why.

The “clincher”, though, would have to be the extraordinary frequency with which we find unit values in Imperial spelled out as ratios between proximal parts of ancient architecture.

I hope that by now, everyone understands what my model of the Great Pyramid actually represents. The origins of the extended model are simply that the height of the Great Pyramid as it currently stands was given by multiple sources as between about 452 and 454 feet; I originally proposed the value of 452.893421 feet purely because Carl Munck held this number in such high regard, referring to it as a “Holy of Holies” and I thought this interpretation might make him happy.

It was only some time later that I realized myself more about what I was looking at, that this gesture had created a ratio of 1.718873385 x 10 – the value of 10 Morton Royal Cubits in Imperial feet – as the ratio between the whole pyramid and the part now missing.

In other words, I’ve been seeing this “unit value in Imperial measures as ratio” phenomenon since the very beginning of my Egyptological studies, and last saw it as recently as my last Egyptological study, where we find Remen in Imperial as ratio in the data from Mariette for one of the coffers in the Saqqara Serapeum, the ratio between the coffer’s iiner and out length, or even from the raw data, 3.85 m / 2.17 m = 1.214511041 = ~1.216733603.

How do we justify this assessment of the Great Pyramid’s missing section? If we look at the Great Pyramid in its present condition, there is almost 28 feet missing at the top, and yet from bottom to top we see it stripped only of the prized casing material, implying that there was a definite cut-off point some 28 below the projected apex with the pyramid above this level made of a different and presumably prized material that supported the actual capstone. I would quite be surprised if the capstone itself exceeded 7 feet in height.

At any rate, what prompts this post is some initial reflection of the idea of astronomical values being “built into” metrological units.

Being quite surprised to find that later Egyptian dynasties in the Faiyum region seemed to be preoccupied with what is now referred to as the “Faiyum Wonder Number”, I could not come up with an explanation except the desire to emphasize the Half Venus Cycle /Calendar Round perhaps more than had been done overtly at Giza, because 3 / Palestinian Cubit = Faiyum Wonder Number / 10 and 4 / Palestinian Cubit = Calendar Round / 10^n.

What this actually distills down to is the ability to side step the calculations in designing architecture. If we know that the Palestinian Cubit is related to the Calendar Round in such a way via a whole number, if we want to write the Calendar Round architecturally, all we really need to do is select ANY valid whole number of Palestinian Cubits for a proportion, and know that someone can – and hopefully will – come along probing the unknown values with whole numbers, and they will soon find it very easily, because we know that the Calendar Round is built into the Palestinian Cubit.

Likewise, if we want to discuss the Solar Calendar Year, we can use ANY valid whole number of Remens, and the same applies, because the Calendar Year is built into the Remen, and etc.

Ideally then, if we can begin to associate unit values with their related astronomical values, then we may be able to infer the astronomical subject material in question from the unit that was used, regardless of the actual value, because if we stop to notice, the stars are often built right into the measurements themselves.

–Luke Piwalker

Integration and Function of Ancient Mathematics

I am continuing to try to carry out my aspiration of interpreting ancient Greek architecture. At the moment I am pausing just a little to try to think of good subjects for study and good experiments, and to search for further archaeological data.

If the results in the last post of looking at the distances between temple column centers for the Temple of Artemis at Ephesus should seem less than satisfactory, it may be because measuring the distance between centers rather than the distance between the outsides of the columns is still only an experiment; we still really don’t know (I don’t, anyway), whether or not we were ever meant to work with the distances between their centers in the first place.

Likewise it is an experiment in progress whether we were ever supposed to try to read anything into values like perimeter / length or perimeter / diagonal ratios of these temples (or other ancient architecture), although these experiments have gone surprisingly well so far, and may be doing so consistently.

I don’t know if this will help anyone to understand what I do or what I propose, but I’ve been toying with the idea for too long now to not try to make a presentation of it.

In red, the overarching purpose and presumed origins of this mathematics – an inclusive, integrated calendar that encompasses and combines the cycles of the planets with multiple Solar and Lunar Cycles. I am hard pressed to come up with anything else that so readily qualifies as what must be THE greatest mathematical achievement of ancient man.

In spite of lacking evidence in some quarters, the existence or reality of such ancient systems really isn’t that much up for debate. Generally speaking, the Mayan Calendar as we think of it is an actual example of exactly this.

It seems as if it can only ever be little more than isolationist nonsense to observe the detection of traces of coca and tobacco in Egyptian mummies and yet declare that the ancient Egyptians (and others) “couldn’t” have had knowledge or functional understanding of the Mayan Calendar, even if the only way they could have obtained it is from the Maya themselves.

In the green square, we see the ways in which metrological unit values derived from astronomy and calendars are related to one another.

Some of this has been the great surprise that comes from a slightly expanded metrology. By adding just a few metrological values – the Megalithic Foot, the Palestinian Cubit, the Egyptian Sacred Cubit, and the Egyptian Royal Foot / Hashimi Cubit – to accompany the Remen, Royal Cubit, and Megalithic Yard already in use in metrological practice, we find that a great number of ancient architectural measurements are easily accounted for, even in the stringent sense of Petrie’s “Inductive Metrology”.

By rights, Petrie’s method should not actually work nearly as well as it does.

“Inductive Metrology” looks to deduce the unit of measurement that was in use a given situation by looking for the occurrence of units in whole numbers, even as Pearson and Chamberlain are doing with “7, 8, 9 and 10” of their Megalithic “Long Foot” at the expense of both Thom’s work and a more robust and realistic ancient metrology.

The method inherently leaves out the possibility that anything could have measured in a whole number + a fraction of an ancient unit, even though the reality of any substantial dataset makes clear that a single unit in whole numbers is inadequate to explain what the data contains.

Thus the idea of successful “Inductive Metrology” efforts doesn’t seem to sit well at all with the idea of ancient peoples using only one particular metrological unit, and historically, they didn’t. A number of different units are of course attributed to the ancient Egyptians and others, and ultimately “Inductive Metrology” can illuminate their reason for being.

For example, a multitude of Egyptian pyramid passages measure 2 Royal Cubits in width, which is quite easy to spot and was frequently spotted by Petrie. However, given the nature of the data, we might be left with the conclusions that the ancient Egyptians frequently made passages a very simple number of units wide, but made passage heights to be some inexplicably complex fraction like 4 and 3/8 or 5 and 7/16 Royal Cubits high.

The simpler and more comfortable answer may be that they used other units besides the Royal Cubit wherein these complex values of Royal Cubits will have equally simple values. More likely the height of such passages may prove to be equally simple numbers of other units, such as 6 Remens or 4 Palestian Cubits or etc.

Again, the metrology of the King’s Chamber in the Great Pyramid itself seems to be 10 Royal Cubit wide by 20 Royal Cubits long by 18 Hashimi Cubits high. The height may be interpreted by some as “11 Royal Cubits” but it can be seen as 18 Hashimi Cubits / Egyptian Royal Feet, which is also the unit of the floor diagonal.

The Great Pyramid King’s Chamber informs us that the Egyptian Royal Foot / Hashimi Cubit is the diagonal unit to a 1:2 rectangle measured in Royal Cubits, just as the Megalithic Yard is the diagonal unit to a 1:2 rectangle measured in Remens.

Thus the surprising thing is that “Inductive Metrology” actually can work if we only avail ourselves of a few more historical units, and the identification of applicable units in a given situation is another criteria we can apply to help guide our interpretive efforts, which may be exactly what we, as interpreters, were intended to do. When in doubt we can look for values that make good metrological sense this way as the possible foundation of a architectural design.

We can begin to look on metrology then like having a set of a dozen master keys or “skeleton keys” and say that whatever locked door (unidentified architectural measurement) we encounter, one of the twelve keys should open it.

When we go to ask where we are supposed to acquire such a set of master keys, the answer is obviously from metrology, and rather orthodox metrology quite often goes a great distance toward that end.

Several of the big surprises in relatively recent months have graphically illustrated how we might come into possession of a full set of these metrological “keys” even if we only have one unit at our disposal. The geometric relationships of units through the geometry of squares and rectangles seems to go much further linking different unit values that even researchers like John Michell may have ever dreamed, and it seems a great pity that few if any seem to have ever really followed his leads in this direction, in spite of the considerable renown, affection and loyalty often afforded to Michell.

How a rectangle measuring 2 by 1 generates the square roots of 2, 3 and 5, and how it relates to and helps to define ancient Egyptian measurement. Almost 50 years ago, John Ivimy, Euan MacKie and others brought up these very straightforward unit relationships in defense of Alexander Thom’s Megalithic Yard.

Take any established unit then and begin applying simple square roots from the basic geometry of squares or rectangles, and the collection of “master keys” in our possession should being to complete itself. If we do this, even if it is our first effort at interpretation, we can begin our efforts with a relatively complete set of “keys”. In this manner, any example of ancient architecture may lavish upon us the very tools (“keys”) we need for its interpretation.

The biggest recent surprise of all, however, metrologically speaking – discovered with guidance from Geoff Bath and his astute emphasiss on diameteral vs circumferential units – is the dramatic and precise unification of ideal units through the elementary geometry of circles and the ratio Pi or 2 Pi, which link diameter or radius to circumference of circles.

This should not have come as a surprise, but I think that in the “old days” even when we considered the most important number of all to be 2 Pi because this seems to be the perimeter / height ratio of the most important and majestic Egyptian pyramid of all, the Great Pyramid, we had enough faith in this number that I think sometimes we took it for granted, which unfortunately meant sometimes failing to apply it as a mathematical probe even for as obvious a method as this would be.

As you the reader might guess, with the Pi or 2 Pi relationship between various historical units of measure coming as a major surprise, the ideal values determined for these units were not predicated on Pi or 2 Pi or circular geometry, but on their interactions with different major mathematical constants like 1.177245771 or 1.622311470, or on the likelihood of their actually being present in real-life situations.

What essentially qualified these ideal unit values in the first place is essentially their relationships to one another, even though at the time I don’t think anyone realized that that was what was happening because we had little or no idea that some of the numbers involved like 1.177245771 might be actual metrological units. Even for the incalculable amount of work I’ve done with the number 1.177245771 for 20 years, it is to the credit of Harris and Stockdale for recognizing any value like this as a metrological unit and as an astronomical data recovery tool.

At any rate, the designations of the four sides of the green square show us four different ways that a larger collection of metrological “keys” can be obtained from a smaller set, and collectively this is another recent revelation that there seems to be a “core group” of major historical metrological unit values that are so well chosen and so well integrated as to make this possible, even for what an absurdly demanding requirement it might otherwise be.

The designated sides of the blue square indicate the sciences that are served by the numbers originating from the achievement of an including integrated calendar. The very same numbers serve not only astronomy, but metrology, geometry, and geodesy as well, so that we can communicate effectively in all of these fields using the very same numbers, and indeed the individuals who possessed mathematical skills may have often worked in multiple disciplines, such as the 18th dynasty “astronomer-architect” to Hatshepsut, Senenmut.

The desire to have such interrelated units of length measure can probably be seen in the selection of the 5280 foot ~5280 ft mile, which facilitates the use of multiple astronomical expressions in geodesy for purposes of geodetic modelling at ratios like 1 Royal Cubit:1 Mile and so forth, that allow us to do things like writing the size of the earth in miles into architecture effectively in some other unit than the mile entirely.

(If anyone should doubt that this was taking place, please take a good look long at the data for the Bent Pyramid for starters).

Generally speaking, the circumference in earth in miles is an amazing numerical value that is highly amenable to geodetic modelling with a wide variety of ancient units, which again would not even be possible without someone at some point in time having designated just such a mile value.

These principles also relate once again to the role of basic geometry expressions as facilitators and coordinators of a core group of ancient units, which would seem to be why we find geometry expressions like 2 Pi (circumference / radius) built into ancient Egyptian pyramids, most notably but not limited to the Great Pyramid.

Essentially, circular geometry is the best thing that ever happened to ancient metrology, and even ancient structures which are not circular (like the Great Pyramid) seem very eager to “talk” about it.

As a unifying mathematics that links together and serves all of these diverse functions, the utility and applicability of our number system is vast, and we can see exactly why it might have been so attractive to ancient mathematicians for them to go through the trouble of actually working it out and using it.

Even when Munck’s “geomathematical” paradigm seemed to collapse around us, I declared that someday I would return to this work because Munck’s mathematics is elegant and eminently logical. I knew even then that if even if we had the wrong applications, we most likely had the right numbers.

Thankfully, this work has managed to come a long way since then.

–Luke Piwalker

The Temple of Artemis at Ephesus

I am by now a veteran of extensive studies on Egyptian, Mayan and Megalithic architecture, but lately it occurs to me that the subject of Greco-Roman architecture has been much neglected in the course of that. As I ponder whether to try to plunge more deeply into the subject, I think that if it’s possible I’d like to begin by aspiring to be something a specialist on temples devoted to Apollo, Artemis and Zeus (or their equivalents).

There’s something of a head start in that direction from Raneiri’s data, and the parallels between the temples of Apollo at Didyma an Artemis at Sardis therein seem truly noteworthy. It’s as if the two were designed with each other in mind, or drafted from something of the same design.

That being the case, and the Temple of Artemis at Ephesus being one of the most famous Greek temples I can think of, we must be fortunate that there seems to be some data available from John Turtle Wood’s report (a plan can be found here).

From the plan, we have a major length of 418′ 1.5″ = 418.125 ft and a major width of 239′ 4.5″ = 239.375 ft, along with a minor length of 342′ 6.5″ = 342.5416666 ft and minor width of 163′ 9.5″ = 163.7916666 feet.

My suspicion is that the raw 418.125 ft value may mean 418.2822014. It’s the square root of (360 x 486), but more importantly, since it is the square root of a valid whole number, this figure would be in the putative Egyptian Sacred Cubit (418.2822014 / 2.091411007 = 200 Egyptian Sacred Cubits). (The value 418.2822014 x 10^n would seem to be another of Munck’s introductions and may have something of a history in his “geomathematical” proposals).

Probably the first guess as to what 342.5416666 should be would be the reciprocal of 24 Remens: Remen 1.216733603 x 24 = 29.20160646; 1 / 29.20160646 = 342.4469134 / 10^n (288 Greek Feet = 292.0160647 ft).

Oddly enough, the other two parameters don’t seem quite so self-explanatory. so we will try to look to some data projections for possible guidance.

From the raw data, the major diagonal would be approximately sqrt ((418.1256^2) + (239.375^2)) = 481.7980988 ft and the minor diagonal approximately sqrt ((342.5416666^2) + (163.7916666^2)) = 379.687376 ft; the major perimeter would be approximately (((418.1256 x 2) + (239.375 x 2)) = 1315.001200 ft and the minor perimeter approximately ((342.5416666 x 2) + (163.7916666 x 2)) = 1012.666666 ft = approximately 1000 Greek Feet.

I should pause here for a moment to point something out. Did anyone spot it?

379.687376 / 2 = 189.843668 = ~Half Venus Cycle 18980 days / 100, and in fact the primary representation in use with these numbers seems to be 18983.99126.

As for the identity of ~1315.001200 ft, I’m not really certain, but it does bear resemblance to some geodetic possibilities (24901.55 x 5280 = 1314.801840 x 10^n), as well as bearing resemblance to a quantity in Inverse Greek Feet (13333.33333 / 1315.001200 = 10.1394077; 13333.33333 / 10.13944669 = 1314.996147 = (24905.23006 x 5280) / 10^n).

I’m not certain what 481.7980988 is supposed to be – it much resembles the height of the Great Pyramid, but the projected figure may be just a little too high to be that. Generally it is in the neighborhood of (12 x 10^n) / Circumference of earth in miles, and apparently closest to the Equatorial circumference figure.

The major perimeter / diagonal ratio would be about 1315.001200 / 481.7980988 = 2.729361538 (sidereal month = ~27.3 days) and the minor perimeter / diagonal ratio about 1012.666666 / 379.687376 = 2.667106495

Note that the temples of Apollo at Delphi and the Megaron at Troy gave Length / Width ratios of 2.666666666 in Ranieri’s data, and the temples of Apollo at Didyma and Artemis at Sardis gave perimeter / diagonal ratios of 2.665588198

The later figure at least, 2.665588198, is suspected of meaning 106.7438159 / 4 = 2.668959398.

Here is an interesting trick that I wasn’t aware of: if we take the minor perimeter of the Temple of Artemis at Ephesus to be 1000 of the now standard (long) Greek Foot of 1.013944669 (12.16733693 / 12) ft, and the diagonal to represent the B version of the “Mayan” Venus Cycle (a simple way to remember this is 5 / (1.622311470^2) x 10^n = 18997.72194 Calendar Round B = Half Venus Cycle B, 18997.72194 x 2 = 37995.44388 Venus Cycle B)…

(It exceeds the canonical value of 18980 noticeably but there are reasons it exists, some of which I have shown before including when talking about certain approximations being mathematically “justified”, and the ancient seem to have made the best of it quite well).

1013.944669 / (379.9544388^1) = 2.668595404 = 10.67438159 / 4, just what we suspected the ratio might be for the temples at Didyma and Sardis, and

1013.944669 / (379.9544388^2) = 7.023461583 x 10 — and yes, that is our “Egyptian” Faiyum Oasis Wonder Number of 1 / (3 / Palestinian Cubit 2.107038476), which itself has the A version of the Half Venus Cycle / Calendar Round built into it (4 / 2.107038476 = 18983.99126 / 10^n).

That is absolutely remarkable for someone to find a use for the square of the Half Venus Cycle like that, let alone one so much in context. Note how they have seemingly combined just the right numbers for us to discover that, and that what this is all about – looking for combinations of numbers in architecture that show deliberateness, insight and intent and help us to understand what was on the architect’s mind, no matter how many other perspectives (such as Ranieri’s) might also be applicable.

Something that might be of interest is that backing up a bit to take take a look at the length / width ratios, the raw values from the data are

418.125 / 239.375 = 1.746736292
342.5416666 / 163.7916666 = 2.091325363

Sine we know there is often a premium on expression of metrological unit values in “modern” feet as ratio, we might suspect these two be of being 1.752096338 (144 Remens / 10^n) and 2.091411007, the putative Egyptian Sacred Cubit in feet; however it’s also possible that these are both two expressions from circular geometry (another major ingredient of our numbers and formulas), namely the reciprocal of the Radian (1 / 57.29577951 = 1.745329252 / 10^n), and 2/3 of Pi = 2.094395102.

Carl Munck seemed to be quite observant of 2/3 Pi; I prefer to work with 1/3 of Pi and one of the reasons is the possible conflation of the Sacred Cubit and 2/3 Pi, but 1/3 of Pi is after merely half of 2/3 which in itself is enough to cast importance on 2/3 Pi.

(Depending on our inclinations and sensibilities, we can also take 2/3 of Pi to be an alternate Sacred Cubit scaled to Morton’s Royal Cubit although I have not yet had to do so in this work unless trying to project a spectrum of unit values as troublingly complex as John Neal’s).

Let’s hope with all that we have created enough inroads that the route from there to a completed model of the basic floor plan values will be a fairly direct one.

There is something else that may jump out as from Wood’s plan of the temple at Ephesus, where he has laid out some of the distances between columns

28′ 8.5″ = 28.70833333 ft
23′ 6″ = 23.5 ft
20′ 4.5″ = 20.375 ft
19′ 4″ = 19.33333333 ft

None of these figures seem to reduce well to Greek Feet in any ordinary way.

23.5 ft may be an expression in Megalithic Feet (23.5 / 2 = 11.75, 10 Megalithic Feet = 11.77245771; Harris-Stockdale Megalithic Foot given as 10 x ((sqrt 2) / 12). 19.33333333 could be several things; one is possibly the figure 1.618829140 x 12 = 19.42594968 ft that seems thus far to recur in ancient Greek architecture.

19.42594968 was first found tentatively at the Rio Bec site in Mexico and some time later it was discovered that the number has astronomical significance as the number of seconds in a Venus Orbital Period as represented by the now classic approximation 224.837383.

224.837383 days x 24 hours x 60 minutes x 60 seconds = 19425949.7

Other significant figures roughly near the range of 19.3333333: 18 Hashimi Cubits = 19.21388686 (featured in the King’s Chamber); sqrt 375/100 = 19.36491673; the Cuicuilco Number (Royal Cubit in inches / Hashimi Cubit in feet = 20.62648062 / 1.067438159 = 19.32334950), and possibly at least one other (divisions of the Calendar Round by Pi^2 also tend to be in about the range of 19.23 x 10^n or so).

20.375 ft might be one of several things. One is 24 / 1.177245771 = 20.38656718 = 10.19328359 x 2; another may be 10.17140347 x 2 = 20.34280694.

1.017140347 = 360 / standard Lunar Year 353.9334578 approximating “354” days. It is, so to speak, to the Lunar Year what the Greek Foot is to the Solar Year (365.2000808 / 360 = 1.013944669, (long) Greek Foot.

28.70833333 ft is somewhat mysterious; it’s already not the first time we’ve seen a figure like this in Greek architecture, but whatever it is, the answers back from mathematical probes often try to drift upward to keep trying toward 288 x 10^n.

If we look at the raw ratio estimates,

28′ 8.5″ = 28.70833333 ft
23′ 6″ = 23.5 ft
20′ 4.5″ = 20.375 ft
19′ 4″ = 19.33333333 ft

28.70833333 / 23.5 = 1.221631206; 23.5 / 20.375 = 1.153374233; 20.375 / 19.33333333 = 1.053879310, we see what look like twice the Great Pyramid’s slope length from the base, the Egyptian Royal Foot, and what could be 1.053519238 (1/2 Palestinian Cubit in feet).

1.221631206 x (1.177245771 x 2 = 23.54491542) = 28.80000000

What we actually get for trying to fit the Egyptian Royal Foot in there may not be what we could have hoped for; (1.177245771 x 2 = 23.54491542) / 1.152833215 = 20.443252277; 23.54491542 / 1.152 = 2.043829464; again not everything works, but as often it can take awhile to work out more elaborate designs.

There may be other possibilities to consider like 20.40131232 (an expression in standard Megalithic Yards) = (sqrt 375/100) x 1.053519238; likewise, sometimes when it looks like we’re seeing the Egyptian Royal Foot we may actually be seeing the Double Radian (57.29577951 x 2 = 1.145915590) or 1.148380617 (1 / (Squared Munck Megalithic Yard x 1.177245771).

I also have a couple of equations that imply that if it isn’t taking too much of a liberty with the data, that what looks like 1.053519238 could yet prove to be Pi / 3 = 1.047197551.

Hopefully, what we may may have achieved here already counts as enough discovery for one day.

–Luke Piwalker

The Parthenon: Some Initial Impressions

As I continue to search for previous work I’ve done on ancient Greek architecture, I discover that apparently I’ve never really posted about the Parthenon although I’ve done a little bit of previous work with it.

I’ve been using Angelopouolos’s diagrams for that. Of course their figures aren’t identical but two other sources provide general corroboration of his figures and help establish the data he gathered himself as sufficiently accurate and reliable.

It’s possible that the Parthenon makes a very good case in point for the problem with Greek Metrology. For some of its most basic proportions, we can see the use of the Greek Foot more clearly than ever (another probable vote of confidence for quality of the data used), but even for these most fundamental measures we do not seem to see it used consistently, which probably means an importation of units that is beyond the understanding of Wikipedia’s source on ancient Greek Metrology.

These basic proportions are

69.589 m = 228.3103675 ft = ~225 Greek Feet
59.087 m = 193.8549869 ft = not Greek Feet?
30.935 m = 101.4927882 ft = ~100 Greek Feet
21.75 m = 71.35826772 ft = not Greek Feet?

228.3103675 is suggestive of 225, this is one of the classic sources for my ongoing remarks that the Greeks seem to have an inclination toward the use of 225 Greek Feet in Imperial.

71.35826772 does not seem to be related to the Greek Foot in the Inductive Metrology sense. Tolerating an error of all of about 8 inches would allow 193.8549869 to be 192 Greek Feet, and about 7 inches in the event of the short Greek Foot; thus this figure may not be in Greek Feet either.

One of the most dramatic things to have emerged from earlier work is that

“69.589 / 59.087 = 1.17773791189 = 11.77245771 I presume.” (Ancient Measures forum, Feb 15, 2020).

I also commented that “On the end the ratio is 30.935 / 21.715 = 1.424591296 – Don’t tell me it’s the Tikal wonder number, 1.424280268? I’ll have to expect (Pi/3) here to decompress it…”

It might turn out to the Faiyum Wonder Number (3 / Palestinian Cubit 2.107038476 ft = 1.423799344) as well, but whatever it is it may be an important key.

It was also suggested that 

“Dimensions given at end inside 2nd row of columns 

21.715 m / 1.68 m = 1.292559524 = 1.290994449?” 

These equations were also given as possible suggestions:

59.087 / 21.715 = 2.720122335 = 2.720174976?
69.589 / 30.935 = 2.249523193793 = 224.8373803?
69.589 / 21.715 = 3.204651162790 = 3.202314486 = 64.04628973 / 2?
72.59 / 69.589 = 1.043124632 = 1.047197551 = (Pi / 3)?
72.59 / 59.087 = 1.228527426 = 1.2328088888 = 2 / 1.622311470?
72.59 / 30.935 = 2.346533053 = 2.354491542 = 1.177245771 x 2?
72.59 / 21.715 = 3.342850564 = 3.346257611 = 1.673128806 x 2?
72.59 / 59.89 = 1.212055435 = 1.216733603?? 

At least half of that may be correct, and we would have (Pi / 3) where we expected it to work with a Wonder Number. The Faiyum Wonder number has an important but limited run with a series from from it and (Pi /3) to about (Pi / 3)^6. I might be inclined to keep giving equal credence to the Tikal Wonder Number for now.

I was going to suggest that maybe the confusion over the true meaning of “225 Greek Feet” owed to a preference for a different Venus Orbital Period (about 225 days) value such as possibly VOP C, but VOP C doesn’t seem to go well with the long Greek Foot, and perhaps not well with the short Greek foot either, which may narrow it down to VOP A 224.8373808 or VOP B 225.

So far I am working with the premise that the preferred Greek Foot is the long one until forced to concede otherwise; if this bears out it may also help to clarify exactly what was intended.

It was noted that 227.8078955 is able to tap into the “Best Lunar Month” value.

227.8078955 x 360 = 1 / 1.219350967; 227.8078955 x (360^2) = 29.52390326

That astronomical gesture might be something else that could have made some of Ranieri’s models come out somewhat strange?

I”m not sure how pertinent they are, but these observations from the original proceedings were interesting (SMMY = Squared Munck Megalithic Yard = 9 / standard Remen 1.216733603)

“1.873644839 / SMMY = 2.533029594 = (sqrt (sqrt 6586.899509)) / 2

(1.177245771 / Pi) / SMMY = (sqrt (sqrt 6586.899509))”

These are reminiscent of some recent observations about other Greek Temples and the Saros Cycle of 6585.3211 conveyed through square roots or other root functions like root 4 (~square root of the square root of the Saros) as seen here.

There was also the intriguing suggestion that “1.415733832 x 4 = 5.662935328 for the Temple of Olympian Zeus” might have been the number that the “Bat Palace” at Tikal was trying so desperately to convey. I don’t know if I’ve ever followed up on that, although right in the middle of trying to learn a new architecture may not be a great time to do it.

The diagonals of these two rectangles would be approximately

sqrt (69.589^2 + 30.935^2) = 76.15512554 m = 249.8527741 ft, a bit too large for a geodetic figure (?) and

sqrt (59.078^2 + 21.75^2) = 62.95452791 m = 206.5437287 ft, just a bit large to be the standard Egyptian Royal Cubit, but could be the rarely seen long Egyptian Royal Cubit?

206.5437287 / 12 = 1.721197739; long Egyptian Royal Cubit = 1.718873385 x 1.000723277 = 1.720116607 ft

So we are seeing 76.15512554 again only this time in meters, and in fact there are a few more figures involved that can catch attention even when in meters, so this may also be an opportunity to explore ancient meters and how the Greeks used them, although I have few expectations that any ancient persons were able to use a single value for the meter consistently.

In context, although it’s very tempting indeed to take these 7.6-something figures and make 7.599088770 of them, metrologically this involves the short Greek Foot, but because of the prevalence of the long Remen (1.2 long Greek Feet) in Egypt and because I am going to use the long Greek Foot in Greece for as long as I can away with it, the opening bid should probably be 1/16th of 100 long Remens, or (100 x 12.16733603) / 16 = 7.604585019 ft, or 6.25 Remens if Petrie isn’t looking over our shoulders to make sure we are hunting for whole numbers of metrological quanta.

I think I will leave it at that for now until I can find some deeper insights on the subject to share.

–Luke Piwalker

The Temple of Demeter at Eleusis (Again)

I continue to try to get a firmer grasp of ancient Greek architecture and its metrology, and of why some of these sites are giving me trouble. I’ve posited a number of possible reasons for the difficulty over the last few posts, but maybe the one that most merits more emphasis is the possibility that that Greek metrology is just plain weird in some ways and poorly understood.

We can go back over to Wikipedia and get a nice, neat metrology all built on the Greek foot, but one serious problem seems to be that the metrology does not consistently work that way with any of the sites that have been looked at so far. Quite the contrary, the minute we start looking at Greek Temple plans and measurements from any source, we begin to see many signs of a diverse set of presumably imported units distinctive from the Greek Foot.

I’m not quite sure what this means. Whereas I have always had to assume a division between ancient advanced math and “common math” – that is, for example, the Mayan Calendar as we think we it was calculated belongs to the “common math” and is the way ordinary people might have used math (just as ordinary people today observe a 365 day year rather than a 365.24 day year), in contrast to the way architect-astronomers might have done math more accurately.

In ancient Greece the “common math” may have been what we see on the Wikipedia page – useful, practical, harmonious – while the mathematics of actual architecture may have been different and more complex.

There may also be something else afoot. It’s too soon to tell, but when I go to do Pythagorean calculations for these examples, I find that the squares of the values are probably catchier than other architecture. We often see this with Egyptian architecture where if we square a side to calculate a diagonal, the squared value may look interesting or intentional, but we know we can’t have everything so we might normally pass on.

The Greek architecture so far somehow seems more worth investigating in this respect, as if where we presume (from experience) that the Egyptians would design a regular structure and then start “tweaking” it in different ways to get more interesting results, it almost seems as if the Greek designs may have generated interesting squares in the designs prior to any “tweaks”?

I discovered at least one other ancient Greek site that we have data for courtesy of Athanasios Angelopoulos that I posted about here under the title of its alternate name, the Telesterion. More recognizably, it is the Temple of Demeter at Eleusis.

In the previous work, the instance of interesting squares for the Telesterion was already noted, but the trend may have continued through the other sites we are looking at. I’d prefer not to wrestle with that subject just now, however, but rather move along and see what we might have missed the first time around.

Something interesting is that I cant seem to find the name Callanish associated with the work. Just when I begin to grow skeptical that the “132.9658800 ft” width of the Temple of Apollo at Halisarna (Kos) might actually represent the “Callanish Number” 1.323891319, we are reminded that the Temple of Demeter at Eleusis has Major Perimeter / Minor Perimeter or Major Diagonal / Minor Diagonal values that calculate at about 1.3238 or 1.3239, again giving the sense that the Greeks were “recycling” important numbers from one monument site to another at least as enthusiastically as the ancient Egyptians.

I really haven’t much idea yet what the diagonal figure 257.0666712 is suppose to represent, but for the other diagonal value 194.1129778 ft, I think I am increasingly confident that it’s what it looks like, namely 120 x 1.618829140 = 194.2594968. We have additional encouragement in this direction from both Stonehenge, where it is implied in the lintel circle that 1.618829140 ft is an actual metrological unit, and from recent advances in ancient metrology, wherein we finally learned that 1.618829140 is a form of the Egyptian Royal Foot / Hashimi Cubit because it is related to them by a whole number.

We already seem to see the Hashimi Cubit value bursting out from a number of places even in the very few Grecian Temples under study thus far.

What Stonehenge seems have actually done is after writing 1.067438159 everywhere as one of its favorites numbers, is turn around and write 1.067438159 again as 1.618829140, which should probably be seen as a short form of the Assyrian Cubit that may come with different rules than the standard value 1.622311470.

We also have several ratios coming out to about 2.828, which doesn’t seem to have mentioned in the “Telesterion” Post. Classically, things that look like this usually turn out to be the Lunar Year written in inverse (reciprocal) form.

1 / 354 days = 2.8248587571 / 10^n, or to try to use more precise, more interactive numbers, 353.9334578 = 2.825389852 / 10^n.

IF that is the correct ratio and IF 120 x 1.618829140 = 194.2594968 is the correct Minor Diagonal value, then 2.825389852 x 194.2594968 = 548.8588109 ft should be the correct value for the Minor Perimeter, calculated at 549.1666666. I am not certain that’s right. There is also 1944/1000 of a Hashimi Cubit = 549.0937032 / 10^n, or 2.107038476 / 384 = 5.487079365, or 46656/1000 Megalithic Feet = 5.492557869, or…

As I say, even a limited collection of whole numbers and metrological units can create numbers in whole numbers one unit that much resemble values in whole numbers of other units, which is the lastest reason why I make no apologies for working with a system that has thrown out most of the whole numbers in literal forms.

Last time around we spotted a possible Saros Cycle reference:

“Another Lunar reference that might have been included here involves 56.314 m = 184.7572178. (sqrt (Saros Cycle / 10) = 6585.3211 / 10) x 360 x 2 = 18476.55395.”

Here, let us note that Saros Cycle 6585.3211 days / 12 = 548.7767583

Then again, the reciprocal of the Greek Cubit (short) is thought herein to be 1 / (Radian / Pi) = 548.3113556 / 10^n, and the reciprocal of the Long Greek Cubit 547.9150613 / 10^n.

Once again, it looks like we may see a brilliant gesture on their part, even if it’s not yet clear exactly what they did.

I don’t think it got mentioned last time but 13.44 / 12.26 = 1.096247961. Things that look so much like 1.096622711 usually seems to turn out to be just that.

From the perspective of my work and methods, the raw value 726.9947507 doesn’t seem to have much relationship to the Greek Foot. 727.2205212 is one similar number that is part of our vocabulary = 1250 Inverse Royal Cubits = (1 / 1.718873385) x 1250. Its relationships to the Egyptian Mystery Unit might offer more clues to possible candidates, but the figure doesn’t seem to be in this unit per se either.

726.9947507 is near to (Pi / 3) x 6939.688 Metonic Cycle (726.722428 x 10^n) and probably other things that we might wish to consider before we declare it a definite expression in Royal Cubits. Some might even wish to consider the square root of the 5280 foot “modern” mile, an ancient reference unit in probably the truest sense of the word as it participates in the system without being directly involved in the system. It’s what gives meaning to many examples of geodetic modelling and allows us geodetic formulas using the Solar Year, Venus Orbital Period, and etc.

The classic is 365.25 x 360 = 131490 and 131490 / 24903.40909, as accurate as some of the maps of the 20th Century. That wouldn’t work if someone hadn’t come up with mile of at least approximately 5280 feet, and the ancients were apparently eager to do for exactly such reasons.

Here is an extra exercise I’ve done with the data. I don’t think I’ve attempted this before, but it appears to give a meaningful result at least in that the diagonals involved seem to be recognizable as probably 72 Pi feet = 226.1946711 and 229.3488809 ft (73.00401618 x Pi), which have a ratio between them of 229.3488809 / 226.1946711 = 1.013944669, or one (Long) Greek Foot in “modern” feet.

So hopefully we have re-established that ancient Greek architecture may use some numbers or perhaps techniques that may be advanced or may at first seem unfamiliar, but it’s probably not as unfathomable as some of the work with Ranieri’s data may try to make it seem, nor is it so remote from what other ancient cultures appear to have been doing with architectural measures and proportions, and astronomy.

–Luke Piwalker

The Taming of the Skew

One possible reason I still can’t seem to make absolute sense of the Greek Temples that Marcello Raineri uses for his examples (see preceding post) could be because I am overlooking some ancient Greek unit of measure or other. With this in mind, I took a look at Wikipedia’s page on ancient Greek measures. However, all that it really tries to tell me me is that ancient Greece was even better at splitting hairs and then naming each individual hair than ancient Egypt.

There are a plethora (pardon) of various unit names, all neatly derived from dactyloi (digits) the same way we have seen units derived from the Egyptian digit, and ideally there isn’t any difference between the Greek and Egyptian digit in the first place.

However, just like Wikipedia’s page on ancient Egyptian measures that are shows unit values skewed upward (remen = 1.22+ ft), apparently in part because of Clagett, the page on ancient Greek measures show unit values skewed slightly downward (Remen = ~1.213 ft) from our norm of about 1.216-1.217 ft, or the Short Remen of about 1.215 ft.

There are several Remen-like figures known of about 1.213 and 1.214, but there probably isn’t much known point in actually taking them to be Remens besides making things more complicated than they already are.

I was about to say that the thing to do would be to throw out all the skewed values in the Wikipdia tables and start all over with a Greek Foot of 12.16733603 inches, but there are several curious things about the tables as they currently stand.

One is that some of the figures are somewhat suggestive of some more mysterious values from Raineri’s paper, and another is that one of the values is suggestive of the Palestinian Cubit.

Here, a pygon = 15.17 inches; 1 Palestinian Cubit x 72/10 = 15.17067703 ft.

Since these units are all so tightly integrated, rather than throw it out we could treat Wikipedia’s page as “More Than You Ever Wanted To Know About the Palestinian Cubit”, including its relationship to some interesting figures like ~1.213.

The Wikipedia table isn’t actually the first hint that the ancient Greeks could have been using a Megalithic Yard value that is closer to the Sidereal Month rather than the established values, which appear to represent the Draconic Month, and that may be significant as well (13.65 in x 2 = 27.3), and if ever learned recently, we already knew that 2.107038476 x 360^2 = 27.30721865 x 10^n (Sidereal Month = 27.321661554 d).

The thing is, such a homogenous system as we glean from Wikipedia for Greek Measurement has little intrinsic purpose in any established terms concerning data storage and retrieval. If they’re all going to be fractions or multiples of the Greek Foot, there isn’t much point. The ancient Egyptian measures seem to show great diversity for the sake of data storage and retrieval and it’s still very difficult to imagine the ancient Greeks not following suit. How the ancient Greeks would have or could have missed out on the integrated bundle of diverse units that we see on display in Megalithic, Mayan or Egyptian architecture is very difficult to imagine indeed.

Why the Greeks and Roman would take archetypal Egyptian measures and alter them would have to be equally mysterious. Rather we might assume they not only inherited remarkably similar measures (dactyloi = digit, Roman Foot = Egyptian foot, etc), but the very same measures.

So, I still don’t know what the Wikipedia data of on Greek units actually represents except “More Than You Ever Wanted To Know About the Palestinian Cubit”, but of course that should include some basic information on why the so-called “Palestinian” Cubit is so Egyptian in the first place. We’ve seen this previously, which gives us some idea why the Palestinian Cubit and Megalithic Yard are both as Egyptian as anything else, and informs us of the nature of the Hashimi Cubit and why it’s important to ancient Egyptian metrology (the last diagram in the panel also explains how the Egyptian Mystery Unit of 1.676727943 ft relates to the Hashimi Cubit).

There is still more to the story of why I am including such units in the ancient Egyptian metrological vocabulary, such as

So how is it that the ancient Greeks should not have an equally diverse vocabulary of metrological units at their disposal when the Greek Foot is 10/12 to the Remen (12 Greek Feet = 10 Remens), but instead ended up with names for all sorts of fractions of the Greek Foot and nothing else? It’s difficult to think of any modern rational person wanting anything to do with any modern equivalent – again, if I said why don’t we call 2 inches a frapplesnoot and 4 inches a dinkledwiff and etc etc etc, you’re probably think I’d lost it completely and I wouldn’t blame you. You’d want no part of it, am I right?

Everybody ready? All together now, “WHY DON’T WE JUST CALL IT 2 INCHES AND 4 INCHES?!?!?” 🙂

Yet what Wikipedia shows is the ancient Greek metrology doing this very same thing, over and over and over.

At this hour then, not only does the nature of Ranieri’s temples still remain somewhat in limbo, but so does the very nature of ancient Greek metrology itself, or at least as according to any orthodox view..

In a way, we were warned – if we follow the metrology in John Michell’s Dimensions of Paradise, there’s a point where the Greek measures seem want to take an uncertain turn, which has never really been explained, but which may obviously relate to a need for diversified measurements for data storage and retrieval purposes.

I believe score is now at Greeks 2, Piwalker 0 in spite of several nice plays from the side with the Wookie in their cheering section.

While that issue simmers on the back burner, I decided to take a prompt from a recent GHMB discussion of the the Saqqara Serapeum to investigate further. I don’t really know much about the Serapeum, mainly because it doesn’t have a pyramid placed over it, and pyramids are enough to demand one’s attention (there also seems to be something of a a shortage of maps showing the Serapeum in relation to Saqqara and its pyramids that helps make it easy to keep overlooking the Serapeum).

There’s an air of weird mystery about the Serapeum, rumors of bovine worship and enormous coffers purported to be for cattle that are more extravagant than even the coffers of pharaohs and so forth. We know those things about the Serapeum of course, but I really haven’t delved into the available metrological data (or lack thereof) for it.

This page, among other noteworthy things, purports to have data on several of the coffers and quotes from both the Isida Project and from explorer Auguste Mariette to say,

“I have measurements for three coffers. One is from Linant-Bey given to Mariette who added it in an addendum in his publication.

The outer dimension of the coffer is 3.85 meters long, 2.32 meters high and 2.32 meters deep. The inner dimension is 3.17 meters long, 1.73 meters high and 1.46 meters deep. The lid is 3.85 meters long, 0.92 meters high and 2.32 deep. The combined weight he calculated is 62 tons.

The Isida Project gives dimensions for two coffers:

Coffer#2, which doesn’t have a lid: outer dimension are 3.8 m x 2.5 m x 2.4 m

Coffer#17: outer dimension: 3.8 m x 2.17 m x 2.3 m.”

There is part of the experiments with Greek metrology where the using standard Remen value of 1.216733603 ft, (Remen / 16) x 18 = 1.368825303, which is very interesting because Raineri’s data gives us “136.8764” ft as the width of Apollo’s Temple at Didyma, and also because 5 / 1.368825303 = 365.2767076. – thus another possible explanation for troubles with Greek metrology could have been the observance of a more accurate Solar Year than the standard Solar Calendar Year, even without giving up the 12.16733603 inch Greek Foot value.

It’s really just another variation on the hopefully familiar theme, 133333.3333 / 365.0200808 = 365.2767076. 133333.3333 is something of a “Solar Year Exchanger” because the natural square root of 133333.3333 (365.1483717) is so near to valid figures for the Solar Year.

We may also want to note what 1/16th of the standard Remen actually is.

1.216733603 / 16 = 7.604585019 / 10^n ((1.216733603 / 16) x 20 = 1.5201917004, which has been proposed to be the corresponding Greek Cubit to the Long Greek Foot.

12.16733603 inches / 12 = Greek Foot 1.013944669 ft; Greek Foot 1.013944669 x 1.5 = Greek Cubit (?) = 1.520917004 ft = .760458501 x 2.

In the Serapeum box figures attributed to Mariette, the figure of 2.32 m recurs (and 2.3 m appears in the data attributed to the Isida Project). We haven’t seen much of 2.32 meters = 7.611548556 ft although it’s been tentatively spotted at Palenque in Mexico and in the Valley of Kings in Egypt, but it could experience some conflicts of interest with 3.6 Palestinian Cubits = 3.6 x 2.107038476 = 7.58338514 (2.312011179 m).

See where this is trying to head for, though, right or wrong?

Could it be that the data from Mariette isn’t reliable? Well, let’s look at our Exterior / Interior ratios a minute:

Again, “The outer dimension of the coffer is 3.85 meters long, 2.32 meters high and 2.32 meters deep. The inner dimension is 3.17 meters long, 1.73 meters high and 1.46 meters deep. The lid is 3.85 meters long, 0.92 meters high and 2.32 deep. The combined weight he calculated is 62 tons.”

Exterior / Interior Length = 3.85 / 3.17 = 1.214511041
Exterior / Interior Width = 2.32 / 1.46 = 1.589041096
Exterior / Interior Height = 2.32 / 1.73 = 1.341040462

Which look a lot like 1.216733603 (typical for Egyptian work to see Remens and Royal Cubits as ratio), the reciprocal of almighty 2 Pi = 1.591549431, and probably (1.676727943 x 8) / 10 = 1.341382354 which we seem to see a fair amount of while working recently with the pyramids of the Faiyum region. This data from Mariette then might actually be trustworthy.

So I have no finished models for any of the Serapeum boxes as yet (and only the dataset from Mariette is relatively complete), but if we are fortunate, Saqqara, Palenque and the Valley of Kings may all be places we can go to learn more about numbers similar to some of those which may pertain to ancient Greek metrology, which is most often the point of bringing up distribution patterns of mathematical values – learning where we might go to find out more.

Certainly some skepticism is due whether the architects of Palenque were actually thinking of what numbers appear in the Valley of Kings (or vice-versa), but again both cultures appear to have been tapping the same pool of astronomy-related numbers for their architecture and any location where we find a particular number represents an opportunity for learning more about it.

While we are looking at the Serapeum boxes, there is at least one other thing that might be worth pointing out.

2.17 m = 7.119422575 = 14.23884514, which is remarkably close to 1.423799349, a Wonder Number that has emerged as seemingly prominent in the ancient architecture of the Faiyum Oasis. As we now know, this Wonder Number is intimately related to the Palestinian Cubit (and in turn to the Half Venus Cycle / Calendar Round). Thus another possible sign that although this number may be prominent in the Faiyum, it is probably not exclusive to the Faiyum, and the same with any other Faiyum Wonder Numbers.

Finally, in terms of “places we might go to learn more about a particular number”, perhaps a more careful comparative study of Greek architecture on my part might help? I’m still rounding up previous attempts to unravel the proportions of Greek architecture, and just happened across this one – apparently I did post at least one post based on Angelopolous’ data then: The Temple of Olympian Zeus

These figures from that page are particularly notable: The first looks like a clear case of 300 Harris-Stockdale Megalithic Feet (using 1.177245771 as HSMF, 300 x 1.177245771 = 353.1737313), and the second we may have seen echoed in Ranieri’s data where we obtained it for the Temple of Artemis at Sardis. It appears to be Equatorial Circumference in Miles / Royal Cubit in Feet: 24901.19743 / 1.718873385 = 1.448692943 x 10^n.

107.61 m = 353.0511811 ft 
44.132 m = 144.7900262 ft

This number looks like another number from Raineri’s data

110.34 m = 362.0078740 ft

This is also from the Temple of Artemis at Sardis, where it is the calculated diagonal length, whereas in Angeloplous’ data it is the length of the Temple of Olympian Zeus.

This is really reminding me a lot of the way the Egyptians recycled important numbers in their pyramid building (we also have accounts of them re-incorporating actual pyramid material the same way).

With that vote of confidence, we can be probably be more certain what the diagonal of Artemis’ Sardis temple was supposed to be, which is outlined in the post on Zeus’ temples,

“110.34 m = 362.0078740 ft = probably 362.1732357 ft”

I recently found occasion to mention that this number belongs among the “Wonder Numbers”, even if it’s a little shy in front of 2 Pi, 1.622311470 or 1.177245771 – not the most wonderful Wonder Number then, but an important one nonetheless. Students or followers of Carl Munck may recognize the number as one of his introductions and the very same for 1.448692943. The two are related thus: 3.621732357 / 1.448692943 = 2.500000000.

Metrologically, 362.1732357 ft is 216 x Egyptian Mystery Unit (LSR) 1.676727943 ft.

In case anyone noticed the 110.34 figure in meters looking like Eclipse Year / Pi, that actually works to give the best value for the Eclipse Year if the meter here is (Radian^2 / 1000) ft = 3.282806350 ft.

It may be worthwhile then to explore whether 362.1732357 represents by way of analogy the correct recognition of a word on the Rosetta Stone.

–Luke Piwalker

Greeks 1, Luke 0

I had to take down the last blog post on the Temple of Apollo at Didyma. I thought I’d finally got it figured out but I missed one important checkpoint and didn’t realize it until I proceeded to reuse the same formula on the data for the ostensibly equally-proportioned Temple of Artemis at Sardis, relying here on data compiled by Marcello Ranieri in his publication Digging the Archives: The Orientation of Greek Temples and Their Diagonals.

I really don’t know my way around ancient Greek architecture like I’d like to. It took a great deal of work to get to know my way around Megalithic, Egyptian, and Mayan architecture and even then some very important Megalithic and metrological curriculum has only come along the last year as we continue to try to piece ancient math together like a fragmented ancient artifact.

I have made some attempts, both with Raineri’s data, and data from Athanasios Angelopoulos. I posted this here last year based on Raineri’s models, but apparently with little elaboration on the subject on my part.

This image has an empty alt attribute; its file name is raineri_greek_temple_data.gif

There is a great deal that is familiar that comes from the data – I could fill the whole page with various observations and suggestions that may or may not actually fit together – hopefully there are already some readers who can guess what I’d make of some of the raw data such as of course my first guess for the true value of the ratio 1.068000468 will be the much beloved 1.067438159 – and I have an ever-growing list of good candidates for many of the values in the table, but still I’m finding it difficult to arrive at any acceptable let alone definitive interpretations from Raineri’s data.

While we may be able to say that the ancient Greeks were tapping into the same universal ancient math as everyone else, we might yet also have to concede that that they may have been doing so with very clever and possibly rather novel individualistic character as well, even if there is also a remarkable amount of overlap in the tabled data..

The best guess I can come up with so far to account for for the troubles so far is that in Raineri’s examples, is that the Greeks are doing something distinctly different in their architectural math than everyone else.

What is it? If I knew that, I might have finished models from Raineri’s data.

Ranieri has put some focus on Pythagorean triangles in his half dozen examples, but we’ve met those before in Thom’s Megalithic designs and they’ve never resulted in insurmountable problems.

I wrote this in my notes today:

1. The work of Harris and Stockdale highlights the use of a single unit as a data retrieval key for recovery of astronomical data.

2. I have complained of a perplexing and possibly somewhat uniquely Greek expression of “Venus in Greek Feet”, which may belong to an analogous category as 1, where we see various “Lunar Data in Megalithic Feet”.

With a great deal of good fortune, the vital clue may be in there. I will be days redoing calculations to see if things will succeed by being more observant of these points, but I began investigating how important astronomical values other than Venus might be written in Greek Feet, and there might be some helpful surprises.

Partly they are surprising because I wasn’t aware of them even though normally I don’t find it necessary to work in Greek Feet because I use Remens and work with x 12 or / 12 as a mathematical probe, which technically should be the same thing because 12 Greek Feet = 10 Remens.

In my mishap with the Temple of Apollo at Didyma with this false set of projections, the suggested diagonal length of ~(1 / Pi) x 1000 = 318.309886 is, as you can see by looking at the table, closely based on the data from Raineri where the calculated value is 318.3669447 – and could be accurate even if the Length, Width and Perimeter values I built around it are incorrect.

TEMPLE OF APOLLO AT DIDYMA
Length: 288.0000000 ft
Width: 136.6847370 ft
Diagonal length: (1 / Pi) x 1000 = 318.3669447 ft
Perimeter: (1 / 1.177245771) x 10^n = 894.402992 ft

Another way of explaining it might be that the length, width and diagonal are actually correct and the diagonal may be wrong, and rather than the reciprocal of Pi could be what amounts to writing the Apsidal Precession Cycle in Greek feet.

sqrt ((288.00000000^2) + (136.6847370^2)) = 318.7894561 = ~Apsidal Precession Cycle 3233 days / Greek Foot ~1.0139 (long version) / 10.

It’s a difficult call to make then without having a better sense of what may be typical for Greek Architecture, and the Apsidal Precession Cycle, unless no one is looking for it carefully enough, generally seems often sporadic until it’s hard to be sure someone is referring to it until we find a situation like Oxkintok in Mexico where someone seems to be pouring buckets of it over our heads. Not a great leap that the astronomer-architects there may have rightly considered themselves specialists in it.

I’m also a little disoriented because my last series work with Angelopoulos’ data was a year ago and I’ve forgotten most of it since it was hundreds of thousands of equations ago by now, but I can’t find any notes yet mental or written that suggest any of his data was so problematic, which tries to imply there is some problem with Raineri’s data instead, but each of his sources should be consulted carefully before proposing that as a solution, and furthermore there may really be something to the two previous points quoted, about trying to apply the Greek Foot a bit more like we would apply the Megalithic Foot analytically.

So what would this actually look like? Well, we can do a few experiments, and we’ll just use 1.0139 as the (long) Greek Foot for the raw calculations.

Actually, this is data that belongs in tables for ease of overview, but for now let’s look a few examples and at least try to see if we get intelligible results.

For background, astronomically speaking, we can see the Greek Foot itself of about 1.0139 in “modern Imperial” ft as essentially the division between a 365 calendar and a simplified 360 day calendar: 365/ 360 = 1.013888888.

Saturn Synodic Period about 378 days / 1.0139 = 3.728178321; there are several distinctive constants this might be. Saturn’s Orbital Period of about 10759 days / 1.0139 = 10.61079699, which looks much like the reciprocal of 30 Pi.

As mentioned, 225 Greek Ft, a possible homage to the Venus Orbital Period of ~225 day may have been noted as a recurring phenomenon in Greek architecture; the Venus Orbital period written in Greek Feet would look roughly like 225 / 1.0139 = 221.9153763 = ~887.6223994 / 4; Venus’ Synodic Period seems to be already peeking out through the data in Imperial as both the width of the Temple at Locris, and the inverse perimeter of the Temple at Troy.

The Metonic Cycle written in Greek Feet would look something like 6939 / 1.0139 = 6.843870204 x 10^n; this is near to 1/2 of 13.68774041, and is the reciprocal of 1.461161551, resembling the length of the Temple at Locri, as well as resembling the Sothic Cycle and a figure involved with the Hipparchic Cycle.

The Saros Cycle written in Greek Feet would look something like 6585.3211 / 1.0139 = ~6.5 OR about 4 x 1.622311470.

Interestingly, Mars 780 in Greek Feet is about 769.3066377, which is (5 / 6.499358974) x 10^n.

I think we already know this one? “Mayan” Calendar Round 18980 / 1.0139 = 18719.79485 = 224.6735382 / 1200.

Just some examples of basic exercises in learning to recognize major astronomical expressions written in Greek feet, in case that’s what they were doing, and in case that’s what’s making their architecture difficult to read.

Perhaps something else to watch out for – the value 326.850394 in the table is a little perplexing. It resembles the 120 Megalithic Yard outer sarsen circle perimeter at Stonehenge, but with an oversized unwanted/unneeded Megalithic Yard of 326.850394 / 120 = 2.723753283, unless it’s the “Lintel Megalithic Yard” from Stonehenge of 2.725105951 ft (outer lintel circle diameter / 120).

I’m not certain how or why the Greeks would be using this, but it may be a possibility. That’s one thing I may be able to say about Raineri’s data for his six detailed examples is that while much of it does appear to be in Greek Feet even in the Petrie “Inductive Metrology” sense, not all of it does, and some other unit that is fundamentally different from the Greek foot may also have been in use.

Judiging by these examples, the ancient Greeks do seem to have been aware of the Hashimi Cubit value, and hence may have inherited the Royal Egyptian Foot in some form or other, just as much of Greco-Roman metrology makes it appear as if the Greeks and Romans inherited the Remen from the Egyptians.

Hopefully as with other areas of ancient architecture – Megalithic, Egyptian, Mayan – persistence and determination and a broader overview will reveal some of the “routines” that might have been at work in their designs.

–Luke Piwalker

Design a site like this with WordPress.com
Get started